好久没更新了，又毕业工作了。DDPM推导是理解diffusion必过的一关，感觉写成博客更容易让我自己清楚整个推导过程。

首先要搞清楚问题的定义，我们使用diffusion是想要生成图片$x_0$，这个$x_0$是通过采样得到的，和文本生成一样，我们需要采样来保证生成的随机性，所以我们的目的是知道$x_0$的分布。具体得到的方法就是通过加噪和去噪完成。首先是加噪过程，在DDPM论文里叫作forward process(前向过程)或者diffsuion process（扩散过程）：

经过$t$时间步的加噪，我们将图片$x_0$加噪为了$x_t$，而$x_t$是服从正态分布$x_t\sim N(0,1)$。在每一个时间步我们都要加上高斯噪声，直到最后$x_t$是完全服从标准正态分布。

然后是去噪过程，我们将$x_t$去噪为$x_0$，在DDPM论文中叫作reverse process（反向过程）：

也就是从完全的噪声$x_t$去噪到生成的图片$x_0$，也就是在每一步我们都要进行采样。

下面这个原论文的配图很好地解释了加噪和去噪的过程：

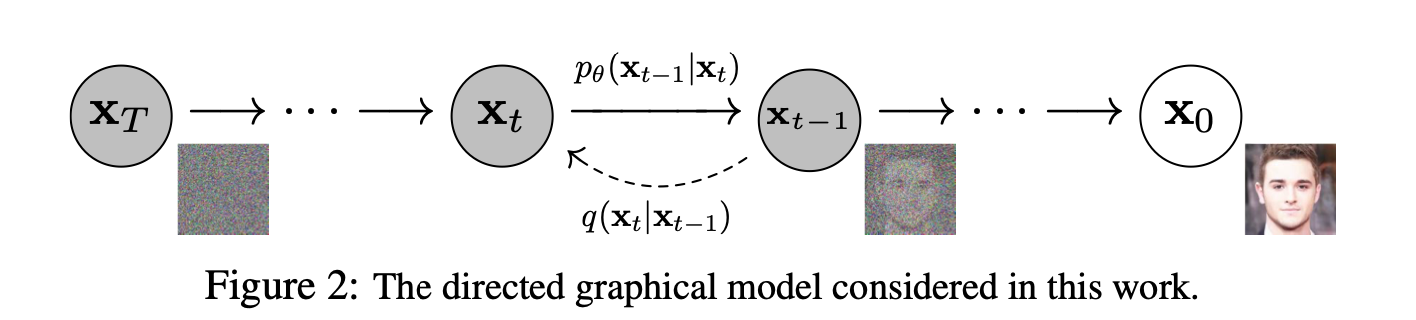
为什么可以从高斯噪声采样出$x_0$?根据中心极限定理，无论原始数据的分布如何，只要样本量足够大，这些样本均值的分布将近似为一个正态分布，这也就理解了可以从高斯噪声（正态分布）中有足够样本量可以还原出生成的图像$x_0$。

我们假设整个过程都是马尔可夫链，也就是说当前状态只会受上一状态的影响，而与更早的状态无关。那么想要完成上述两个过程，需要解决的问题如下：

1. 如何加噪？每一步加的噪声是什么才能保证$x_t$服从标准正态分布？
2. 如何去噪？如果我们能知道每一个时间步的转移概率，比如$P(x_{t-1}|x_t)$的分布，那么我们就可以一步一步去噪到最终的$x_0$
3. 如何把上述的过程用损失表示出来？这样才能训练

加噪过程

先解决第一个问题，要怎么加噪？这个加噪方法怎么得出来的我还真不知道，论文中给出的是：$q(x_t|x_{t-1}):=N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_tI)$。这里将正向的加噪过程的概率记作p，反向降噪过程的概率记作q。写得更简单一些，可以写为：

其中$\epsilon_t$是第t时刻的随机变量，遵从$N(0,1)$分布，上述的做法实际也是重参数化的技巧，将服从$N(\mu,\sigma^2)$的随机变量转为服从$N(0,1)$的随机变量表示。

虽然我们不清楚怎么得到的结论，那么至少能证明这样可以达到$x_t$服从正态分布的效果，接下来是证明：

通过这个简化后的式子我们可以直观理解一下，$\epsilon_t$相当于t时刻的高斯噪声，虽然每个时刻的$\epsilon$都服从$N(0,1)$，但它们的取值是不一样的，每一个时刻都会重新进行采样，这也是diffusion模型相比于GAN和VAE这样的模型更好的地方，就是每一步都引入的随机性。$\sqrt{\beta_t}$是加入噪声的权重，$\sqrt{1-\beta_t}$是保留上一时刻$(t-1)$图像的权重，理论上$\beta_t$的值在0到1之间，$\beta_t$越大加入的噪声越多，保留的上一时刻的图像越少。在DDP《 论文中，$T=1000$，$\beta$线性增长，由$10^{-4}$增长到$0.02$，$\beta_t$的值始终比较小，接近于0，保证每次加入的噪声不多，会先比较小再逐步变大。这一点在之后代码实现相关详细讲一下。

为了推导上的方便，将$1-\beta_t$写作$\alpha_t$，那么根据马尔科夫链的性质，我们可以直接使用$x_0$来表示$x_t$，具体过程如下：

已知：$x_t=\sqrt{1-\alpha_t}\epsilon_t+\sqrt{\alpha_t}x_{t-1}$，接下来我们按照数学归纳法，一步一步来展开

接下来的化简就需要用到正态分布的性质，对于正态分布，有以下两条性质：

我们知道$\epsilon_t$和$\epsilon_{t-1}$都是标准正态分布的随机变量，所以可以推出：

这个时候我们可以将其重参数化，用一个标准正态分布的随机变量$\epsilon$来化简得到：

将上述的结论代入原式，可以将原式化简为：

按照数据归纳法，我们可以推导出：

我们为了简化表达，将$\prod_{i=1}^{i-t}\alpha_i$连乘表示为$\bar{\alpha_t}$：

我们可以审视一下(2)式，这样得到的$x_t$分布是否和我们设想的目标一样，接近一个纯高斯噪声呢？根据上述的简化，$\alpha=1-\beta$，而$\beta$的实际取值是接近于0的，$\alpha$的实际取值接近于1，但是依然是小于1的，根据(2)式我们知道,$\sqrt{\bar{\alpha_t}}$这个连乘项会随着时间步的增加趋近于0，而$\sqrt{1-\bar{\alpha_t}}$则会趋近于1，那么经过这个过程，结果是会趋近于标准正态分布的，可以说是和我们的预期相符。

去噪过程

上面的推导过程得出，加噪过程可以直接从$x_0$推导到$x_t$，接下来我们可以再看看去噪过程，去噪过程是否能像加噪过程一样一步到位呢？我们已知(2)式，直接逆推，就能得到一个用$x_t$表示$x_0$的式子，是不是可以直接拿来用呢？

答案是不行的，因为我们是通过$t$步加噪由$x_0$得到的最终$x_t$，然后将这$t$步的加噪等价于一个$\epsilon$最终得到完全的高斯噪声。而当降噪时，我们的$x_t$本身是高斯噪声需要还原为图像，而这个高斯噪声是如何得来的？假设通过(2)式一步到位得到的等价$\epsilon$记为$\overline{\epsilon}$，它和$\epsilon$大概率不是一个$\epsilon$，用苏神的话说，这两者并不相互独立，在给定加噪的$\epsilon$情况下（我们得到的$x_t$）使我们无法完全独立地采样我们假定的一步推导出的$\overline{\epsilon}$。更直白地说，去噪过程的高斯分布不是真正的高斯分布，实际是与图片相关的。

那么去噪要怎么实现呢？我们先和加躁一样，一步一步来：

根据(1)式反过来写，即用$x_t$来表示$x_{t-1}$，可以得到：

在这个时刻，$\alpha_t$和$\beta_t$都是已知的，而唯一的未知量是$\epsilon_t$，如同我们上述的理由一样，这里的$\epsilon_t$并不是加噪声随机取的，而是与下一时刻的$x_t$与$t$相关，这时我们把$\epsilon_t$设置成$\epsilon_\theta(x_t,t)$。也就是说我们使用模型来预测得到此刻的$\epsilon_t$，模型的输入是此刻的$x_t$和时刻$t$，输出的是一个分布，通过这一分布进行采样，我们可以得到上一时刻的图像$x_{t-1}$。

按照上述的原理，这样每一步预测后最终就可以得到生成的图像$x_0$。这样去噪的过程也清楚了。

去噪：作者在论文中表示方差不会影响结果只需要预测均值

损失函数

那么下面的问题主要就是如何设计损失函数以及选择什么样的网络进行实现。

先解决损失函数的问题：

我们的最终目标是得到一个生成图像$x_0$，也就是使得我们得到的$x_0$分布接近于真实$x+0$的分布。也就是最大化$p_\theta(x_0)$，我们通过极大似然估计找到符合的参数$\theta$。

通过去噪过程可以将$p_\theta(x_0)$写为：

需要对每种情况下的$p(x_0)$积分，因为每一时间步都需要采样，从$x_T$到$x_1$有无数种采样可能，式(3)根本无法直接求出。那么我们可以将最大化$p_\theta(x_0)$的问题转换为另一个我们可以求的近似问题，也就是ELBO（Evidence Lower Bound），听说这个转换VAE也有用到，之后再说。

首先需要知道ELBO这个概念，在贝叶斯公式里：

其中：

首先将我们的目标从最大化似然转化为最大化对数似然，对数将乘法转换为加法更好计算求导。

参考🔗： Diffusion|DDPM

生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼