字节春招题目,不知道哪一年。原题如下:
毕业旅行问题
小明目前在做一份毕业旅行的规划。打算从北京出发,分别去若干个城市,然后再回到北京,每个城市之间均乘坐高铁,且每个城市只去一次。由于经费有限,希望能够通过合理的路线安排尽可能的省一些路上的花销。给定一组城市和每对城市之间的火车票的价钱,找到每个城市只访问一次并返回起点的最小车费花销。
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
城市个数n(1<n≤20,包括北京) 城市间的车票价钱 n行n列的矩阵 m[n][n]输出描述:
最小车费花销 s示例1
输入例子:
4 0 2 6 5 2 0 4 4 6 4 0 2 5 4 2 0输出例子:
13例子说明:
共 4 个城市,城市 1 和城市 1 的车费为0,城市 1 和城市 2 之间的车费为 2,城市 1 和城市 3 之间的车费为 6,城市 1 和城市 4 之间的车费为 5,依次类推。假设任意两个城市之间均有单程票可购买,且票价在1000元以内,无需考虑极端情况。
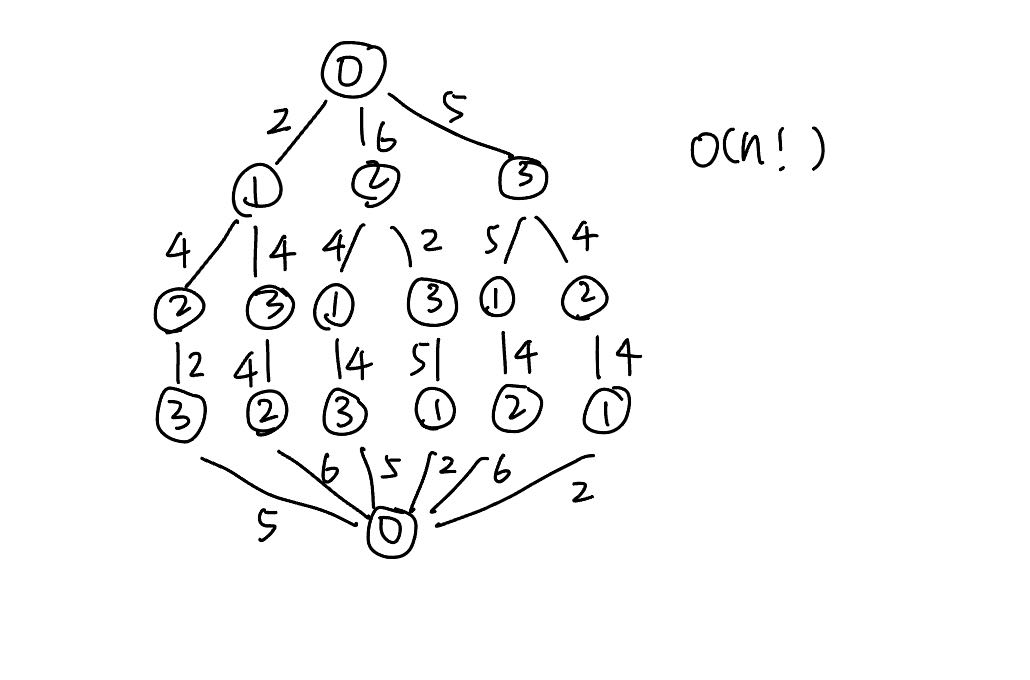
比较自然的想法当然是上dfs。要注意的是最后要成环,这个需要判断一下。因为最终要回到起点,所以具体从哪个城市开始不重要。代码如下:
#include <iostream>
#include<vector>
#include<limits.h>
using namespace std;
int ans=INT_MAX;
int n;
vector<vector<int>> d;
void dfs(int v, vector<bool> visited, int dis){
if(v==0&&visited[v]==true){
ans=min(ans,dis);
return;
}
visited[v]=true;
bool tag=false;
for(int i=0;i<n;++i){
if(visited[i]==false){
tag=true;
dis+=d[v][i];
dfs(i,visited,dis);
dis-=d[v][i];
}
}
if(tag==false){
dis+=d[v][0];
dfs(0,visited,dis);
}
visited[v]=false;
}
int main() {
cin>>n;
d.resize(n,vector<int>(n,0));
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
cin>>d[i][j];
}
}
vector<bool> visited(n, false);
dfs(0, visited, 0);
cout<<ans<<endl;
}
// 64 位输出请用 printf("%lld")
比较悲催的是只能过3/10,看来dfs满足不了要求,我们可以以示例1为例分析一下我们的做法时间复杂度
可以看到,这样很难不超时,那么如何减少时间复杂度呢?随便观察一下,就知道有很多可以剪枝的地方,比如这是个无向图,d[0][1]==d[1][0];再比如0-2-3-1-0和0-1-3-2-0得到的距离是一样的。我们需要一个数组去存储中间结果来减少重复运算,这样就用到了动态规划思想。因为我们需要将所有城市都走一遍并且不重复,所以我们定义 \(dp[n]\{p_1, p_2,...,p_m\}=min(dp[p_1]\{p_2,...,p_m\}+d[n][p_1], ...., dp[p_m]\{p_1,...,p_{m-1}+d[n][p_m]\})\) 其中大括号是所有经过的城市。接下来的问题是怎么表示,我参考题解:🔗旅行商问题解法
因为原题有n小于等于20,这里用bit位来表示是否经过某个城市,总共只需要2的20次方,在int范围内。代码如下:
#include <iostream>
#include<vector>
#include<limits.h>
using namespace std;
int main() {
int n;
cin>>n;
vector<vector<int>> d(n, vector<int>(n,0));
int x=1<<n;
vector<vector<int>> dp(x, vector<int>(n,INT_MAX));
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
cin>>d[i][j];
}
}
for(int i=0;i<n;++i){
dp[0][i]=d[0][i];
}
int ans=INT_MAX;
for(int i=0;i<x;++i){
for(int j=0;j<n;++j){
if(dp[i][j]!=INT_MAX){
for(int k=0;k<n;++k){
int cur=1<<k;
if((i&cur)==0){
dp[i+cur][k]=min(dp[i+cur][k], dp[i][j]+d[j][k]);
}
}
}
}
}
for(int i=0;i<n;++i){
ans=min(dp[x-1][i]+d[0][i],ans);
}
cout<<ans<<endl;
}