题目链接:https://leetcode-cn.com/problems/median-of-two-sorted-arrays/
题解基本思想来源于https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-2/的解法三,只是在他的基础上写写自己的见解。
首先这道题要求的时间复杂度是O(log(m+n))可以猜测到只有二分查找可以达到。按照题解,我们把寻找中位数当作寻找第k小的数的一个特例。
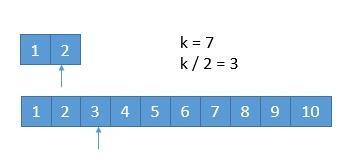
在寻找第k小的数的过程中,我们可以每次排除k/2个数,其过程如下:
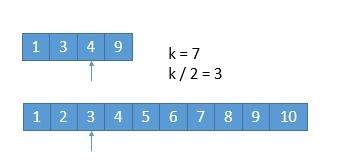
我们比较两个数组k/2位置上的数的大小,可以知道3<4,由此我们知道(1,2,3)一定不是第7个数。由此排除第二个数组k/2个元素,接下来我们继续:
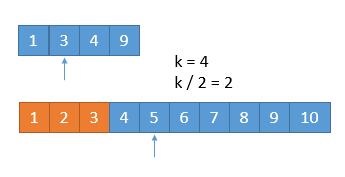
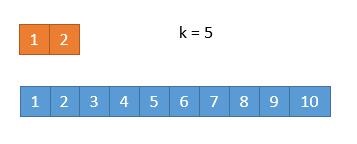
此时我们已经排除了k/2个元素,接下来在数组中寻找的应该是第k-k/2个小的数,所以k从7变为了4。此时我们再比较第k/2个元素,也就是3和5,得到3<5可以知道(1,3)能排除掉。
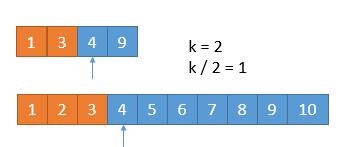
步骤同上,不同的是此时我们比较的4和4相等,此时排除掉任意一个数组的数字都可以。不妨排除下面一行的数组:
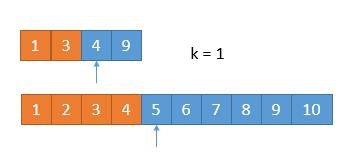
最后的结果为4。
另一种情况当循环进行时有一个数组全部排除,那我们就可以只看这一个数组了,计算更简单:
根据上述的思想来写代码,值得注意的是在总数为偶数的情况下,我们需要找两个数,而在我们循环的过程中,如我们已经找到了第(m+n)/2-1小的数,找到第(m+n)/2小的数只需要再在基础上比较一次就可以,不需要再从头计算。代码实现如下:
class Solution(object):
def getKth(self, nums1, st1, ed1, nums2, st2, ed2, k):
len1 = ed1 - st1 + 1
len2 = ed2 - st2 + 1
if st1 > ed1:
return st1, ed1, st2+k,ed2, nums2[st2+k-1]
if st2 > ed2:
return st1+k, ed1, st2, ed2, nums1[st1+k-1]
if k==1:
if nums1[st1] < nums2[st2]:
return st1+1, ed1, st2, ed2, nums1[st1]
else:
return st1, ed1, st2+1, ed2, nums2[st2]
i = st1 + min(len1, k/2) - 1
j = st2 + min(len2, k/2) - 1
if nums1[i] < nums2[j]:
return self.getKth(nums1, i+1, ed1, nums2,st2, ed2, k-(i-st1+1))
else:
return self.getKth(nums1, st1, ed1, nums2, j+1, ed2, k-(j-st2+1))
return st1, ed1, st2, ed2, x
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
n1 = len(nums1)
n2 = len(nums2)
# tag==True时是奇数,否则是偶数
tag = True
if (n1+n2)%2 == 0:
tag = False
# k为第k小的数,从1开始计数,如果是偶数需要求第k小和第k+1小的数
k = (n1+n2+1)/2
# 之所以这样设计是想减少第二次计算时的重复操作
st1, ed1, st2, ed2, x = self.getKth(nums1,0,n1-1,nums2,0,n2-1,k)
if tag:
return x
else:
_, _, _, _, y = self.getKth(nums1,st1,ed1,nums2,st2,ed2,1)
return (x + y) / 2.0