1.5 Autograd
Pytorch has a built-in differentiation engine called torch.autograd. It supports automatic computation of gradient for any computational graph.
# 以最简单的wx+b为例
import torch
x = torch.ones(5) # input tensor
y = torch.zeros(3) # expected output
w = torch.randn(5,3,requires_grad = True)
b = torch.randn(3, requires_grad = True)
z = torch.matmul(x,w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z,y) # cross entropy:交叉熵
Tensors, Functions and Computational graph
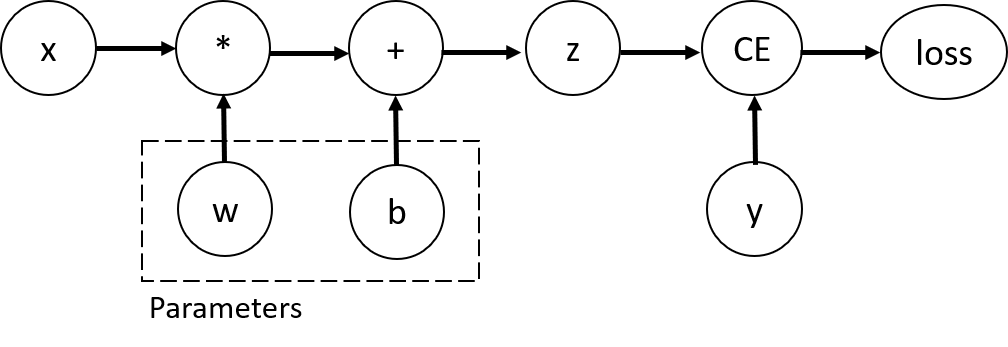
在上图中,w和b是参数,我们需要计算它们的梯度,对于这样的变量,可以将requires_grad设置为True,如上面的代码。也可以在之后用w.requires_grad_(True)来赋值
Function类中可以实现正向和反向传播。
grad_fn存储了每个tensor的属性。
print('Gradient function for z = ',z.grad_fn)
print('Gradient function for loss = ',loss.grad_fn)
Gradient function for z = <AddBackward0 object at 0x7fa36faa5490>
Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward object at 0x7fa36fbd3400>
Computing Gradients
print(w.grad)
print(b.grad)
loss.backward() #求loss对w、loss对b的偏导
print(w.grad)
print(b.grad)
None
None
tensor([[0.3164, 0.3318, 0.1846],
[0.3164, 0.3318, 0.1846],
[0.3164, 0.3318, 0.1846],
[0.3164, 0.3318, 0.1846],
[0.3164, 0.3318, 0.1846]])
tensor([0.3164, 0.3318, 0.1846])
- 只有对requires_grad设置为True且是图中的叶子结点,我们才能求出grad
- 对一张图我们只能backward一次,如果想要多次backward可以:
loss.backward(retain_graph = True)
Disabling Gradient Tracking
默认情况下,所有设置了requires_grad=True的tensors都会track their computational history and support gradient computation.
在一些情况下我们不需要,可以使用torch.no_grad()停止追踪
z = torch.matmul(x,w)+b
print(z.requires_grad)
with torch.no_grad():
z = torch.matmul(x,w)+b
print(z.requires_grad)
True
False
等价的用法还有:detach()
z = torch.matmul(x,w)+b
z_det = z.detach()
print(z_det.requires_grad)
False
There are reasons you might want to disable gradient tracking:
- To mark some parameters in your neural network at frozen parameters. This is a very common scenario for finetuning a pretrained network
- To speed up computations when you are only doing forward pass, because computations on tensors that do not track gradients would be more efficient.
More on Computational Graphs
在图上(DAG,有向无环图),叶子是输入的张量,根是输出张量。
解释Function做了什么:
- 前向传播:
- 计算结果
- maintain the operation’s gradient function in the DAG
- 反向传播:
- 对每个
.grad_fn计算梯度 - accumulates them in the respective tensor’s
.gradattribute. - using the chain rule, propagates all the way to the leaf tensors.
- 对每个
Pytorch中的DAG是动态的,意思是每次运行.backward()时都会动态创建一个DAG,这意味着,每次iteration你都可以改变DAG。
Optional Reading
在很多情况下,我们的loss function是标量数值。但是,在有些情况下,我们的loss function是一个任意的张量。在这种情况下,Pytorch提供Jacobian product计算。
For a vector function 𝑦⃗ =𝑓(𝑥⃗ ) , where 𝑥⃗ =⟨𝑥1,…,𝑥𝑛⟩ and 𝑦⃗ =⟨𝑦1,…,𝑦𝑚⟩ , a gradient of 𝑦⃗ with respect to 𝑥⃗ is given by Jacobian matrix(雅各比矩阵):
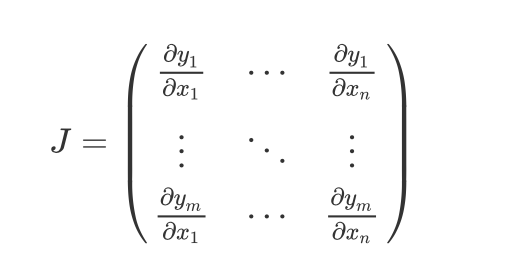
Instead of computing the Jacobian matrix itself, PyTorch allows you to compute Jacobian Product 𝑣𝑇⋅𝐽 for a given input vector 𝑣=(𝑣1…𝑣𝑚) . This is achieved by calling backward with 𝑣 as an argument. The size of 𝑣 should be the same as the size of the original tensor, with respect to which we want to compute the product:
inp = torch.eye(5,requires_grad=True) # eye?
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp),retain_graph=True)
print("First call\n",inp.grad)
out.backward(torch.ones_like(inp),retain_graph=True)
print("\nSecond call\n",inp.grad) # 第二次call的时候accumulate了第一次的结果,所以不一样
inp.grad.zero_() # 想要call的结果一样,需要清零
out.backward(torch.ones_like(inp),retain_graph=True)
print("\nCall after zeroing gradients\n",inp.grad)
First call
tensor([[4., 2., 2., 2., 2.],
[2., 4., 2., 2., 2.],
[2., 2., 4., 2., 2.],
[2., 2., 2., 4., 2.],
[2., 2., 2., 2., 4.]])
Second call
tensor([[8., 4., 4., 4., 4.],
[4., 8., 4., 4., 4.],
[4., 4., 8., 4., 4.],
[4., 4., 4., 8., 4.],
[4., 4., 4., 4., 8.]])
Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
[2., 4., 2., 2., 2.],
[2., 2., 4., 2., 2.],
[2., 2., 2., 4., 2.],
[2., 2., 2., 2., 4.]])
1.6 Optimization
in each interation=迭代=epoch:
- makes a guess about the output
- calculates the error in its guess(loss)
- collects the derivatives of the error with respect to its parameters
- optimizes these parameters using gradient descent
前述代码
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor,Lambda
training_data = datasets.FashionMNIST(
root = "data",
train = True,
transform = ToTensor()
)
test_data = datasets.FashionMNIST(
root = "data",
train = False,
download = True,
transform = ToTensor()
)
train_dataloader = DataLoader(training_data,batch_size=64)
test_dataloader = DataLoader(test_data,batch_size=64)
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork,self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28,512),
nn.ReLU(),
nn.Linear(512,512),
nn.ReLU(),
nn.Linear(512,10),
nn.ReLU()
)
def forward(self,x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = NeuralNetwork()
超参
Read more about hyperparameter tuning.
We define the following hyperparameters for training:
- Number of Epochs: the number times to iterate over the dataset
- Batch Size: the number of data samples seen by the model in each epoch
- Learning Rate: how much to update models parameters at each barch/epoch. Smaller values yield slow learning speed, while large values may result in unpredictable behavior during training.
learning_rate = 1e-3
batch_size = 64
epochs = 5
Optimization Loop
Each iteration of the optimization loop is called an epoch.
Each epoch consists of two main parts:
- The Train Loop: iterate over the training dataset and try to converge to optimal parameters.
- The Validation/Test Loop: iterate over the test dataset to check if model performance is improving.
下面介绍一些在training loop中涉及到的概念:
Loss Function
Common loss functions include nn.MSELoss(Mean Square Error,L2方差),and nn.NLLLoss(Negative Log Likelihood) for classification. nn.CrossEntropyLoss combines nn.LogSoftmax and nn.NLLLoss.
loss_fn = nn.CrossEntropyLoss()
Optimizer
We use SGD(Stochastic Gradient Descent) as optimization algorithm. There are many different optimizers available in PyTorch.
We initialize the optimizer by registering the model’s parameters that need to be trained, and passing in the learning rate hyperparameter.
optimizer = torch.optim.SGD(model.parameters(),lr = learning_rate)
Inside the training loop, optimization happens in three steps:
- Call
optimizer.zero_grad()to reset the gradients of model parameters. Gradients by default add up; to prevent double-counting, we explicitly zero them at each iteration. - Backpropagate the prediction loss with a call to
loss.backwards(). Pytorch deposits the gradients of the loss w.r.t. each parameter. - Once we have our gradients, we call
optimizer.step()to adjust the parameters by the gradients collected in the backward pass.
完整实现
def train_loop(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
for batch, (X,y) in enumerate(dataloader):
# Compute prediction and loss
pred = model(X)
loss = loss_fn(pred,y)
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch*len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test_loop(dataloader,model,loss_fn):
size = len(dataloader.dataset)
test_loss, correct = 0,0
with torch.no_grad():
for X,y in dataloader:
pred = model(X)
test_loss += loss_fn(pred,y).item()
correct += (pred.argmax(1)==y).type(torch.float).sum().item()
test_loss /= size
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avgloss: {test_loss:>8f}\n")
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(),lr = learning_rate)
epochs = 10
for t in range(epochs):
print(f"Epoch {t+1}\n--------------------------------")
train_loop(train_dataloader, model, loss_fn, optimizer)
test_loop(test_dataloader,model,loss_fn)
print("Done!")
Epoch 1
--------------------------------
loss: 1.704071 [ 0/60000]
loss: 1.647429 [ 6400/60000]
loss: 1.579507 [12800/60000]
loss: 1.689828 [19200/60000]
loss: 1.319260 [25600/60000]
loss: 1.669958 [32000/60000]
loss: 1.549762 [38400/60000]
loss: 1.524544 [44800/60000]
loss: 1.748350 [51200/60000]
loss: 1.729603 [57600/60000]
Test Error:
Accuracy: 52.5%, Avgloss: 0.024132
Epoch 2
--------------------------------
loss: 1.641687 [ 0/60000]
loss: 1.592328 [ 6400/60000]
loss: 1.514703 [12800/60000]
loss: 1.639758 [19200/60000]
loss: 1.263364 [25600/60000]
loss: 1.626390 [32000/60000]
loss: 1.504308 [38400/60000]
loss: 1.486582 [44800/60000]
loss: 1.702824 [51200/60000]
loss: 1.693059 [57600/60000]
Test Error:
Accuracy: 53.3%, Avgloss: 0.023426
Epoch 3
--------------------------------
loss: 1.590209 [ 0/60000]
loss: 1.548953 [ 6400/60000]
loss: 1.461693 [12800/60000]
loss: 1.603199 [19200/60000]
loss: 1.221966 [25600/60000]
loss: 1.589929 [32000/60000]
loss: 1.467707 [38400/60000]
loss: 1.457615 [44800/60000]
loss: 1.665463 [51200/60000]
loss: 1.661600 [57600/60000]
Test Error:
Accuracy: 54.1%, Avgloss: 0.022864
Epoch 4
--------------------------------
loss: 1.547178 [ 0/60000]
loss: 1.514135 [ 6400/60000]
loss: 1.418291 [12800/60000]
loss: 1.573686 [19200/60000]
loss: 1.191126 [25600/60000]
loss: 1.560305 [32000/60000]
loss: 1.437528 [38400/60000]
loss: 1.434576 [44800/60000]
loss: 1.633406 [51200/60000]
loss: 1.633844 [57600/60000]
Test Error:
Accuracy: 54.9%, Avgloss: 0.022404
Epoch 5
--------------------------------
loss: 1.510921 [ 0/60000]
loss: 1.484979 [ 6400/60000]
loss: 1.381803 [12800/60000]
loss: 1.549977 [19200/60000]
loss: 1.167677 [25600/60000]
loss: 1.535876 [32000/60000]
loss: 1.412288 [38400/60000]
loss: 1.414794 [44800/60000]
loss: 1.605502 [51200/60000]
loss: 1.609199 [57600/60000]
Test Error:
Accuracy: 55.9%, Avgloss: 0.022015
Epoch 6
--------------------------------
loss: 1.479342 [ 0/60000]
loss: 1.459297 [ 6400/60000]
loss: 1.350616 [12800/60000]
loss: 1.530875 [19200/60000]
loss: 1.149884 [25600/60000]
loss: 1.514547 [32000/60000]
loss: 1.389692 [38400/60000]
loss: 1.396224 [44800/60000]
loss: 1.580315 [51200/60000]
loss: 1.587302 [57600/60000]
Test Error:
Accuracy: 56.6%, Avgloss: 0.021674
Epoch 7
--------------------------------
loss: 1.450816 [ 0/60000]
loss: 1.435704 [ 6400/60000]
loss: 1.322533 [12800/60000]
loss: 1.515100 [19200/60000]
loss: 1.135166 [25600/60000]
loss: 1.496108 [32000/60000]
loss: 1.368966 [38400/60000]
loss: 1.376437 [44800/60000]
loss: 1.557823 [51200/60000]
loss: 1.567781 [57600/60000]
Test Error:
Accuracy: 57.1%, Avgloss: 0.021367
Epoch 8
--------------------------------
loss: 1.424296 [ 0/60000]
loss: 1.413456 [ 6400/60000]
loss: 1.296861 [12800/60000]
loss: 1.501444 [19200/60000]
loss: 1.121897 [25600/60000]
loss: 1.479703 [32000/60000]
loss: 1.350066 [38400/60000]
loss: 1.358520 [44800/60000]
loss: 1.536642 [51200/60000]
loss: 1.550272 [57600/60000]
Test Error:
Accuracy: 57.6%, Avgloss: 0.021083
Epoch 9
--------------------------------
loss: 1.399351 [ 0/60000]
loss: 1.392104 [ 6400/60000]
loss: 1.273390 [12800/60000]
loss: 1.488880 [19200/60000]
loss: 1.109936 [25600/60000]
loss: 1.464471 [32000/60000]
loss: 1.331866 [38400/60000]
loss: 1.341325 [44800/60000]
loss: 1.516436 [51200/60000]
loss: 1.533840 [57600/60000]
Test Error:
Accuracy: 57.9%, Avgloss: 0.020818
Epoch 10
--------------------------------
loss: 1.375886 [ 0/60000]
loss: 1.371588 [ 6400/60000]
loss: 1.251603 [12800/60000]
loss: 1.477427 [19200/60000]
loss: 1.098617 [25600/60000]
loss: 1.450309 [32000/60000]
loss: 1.314592 [38400/60000]
loss: 1.325437 [44800/60000]
loss: 1.497152 [51200/60000]
loss: 1.518209 [57600/60000]
Test Error:
Accuracy: 58.3%, Avgloss: 0.020569
Done!
Further Reading
1.7 Save and Load the Model
import torch
import torch.onnx as onnx
import torchvision.models as models
Saving and Loading Model Weights
Pytorch models store the learned parameters in an internal state dictionary, called state_dict.These can be persisited via the torch.save method.
model = models.vgg16(pretrained = True)
torch.save(model.state_dict(),'model_weights.pth')
Downloading: "https://download.pytorch.org/models/vgg16-397923af.pth" to /Users/alexandreaswiftie/.cache/torch/hub/checkpoints/vgg16-397923af.pth
0%| | 0.00/528M [00:00<?, ?B/s]
To load model weights, you need bto create an instance of the same model first, and then load the parameters using load_state_dict() method.
model = models.vgg16() # we do not specify pretrained=True, i.e. do not load default weights.
model.load_state_dict(torch.load('model_weights.pth'))
model.eval()
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace=True)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace=True)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace=True)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
注意:be sure to call mode.eval() method before inferencing to set the dropout and batch normalization layers to evaluation mode. Failing to do this will yield inconsistent inference results.
Saving and Loading Models with Shapes
如果我们还想要保存模型的类别,我们可以传入model而不是model.state_dict()
torch.save(model,'model.pth')
we can then load the model like this:
model = torch.load('model.pth')
注意:This approach uses Python pickle module when serializing the model, thus it relies on the actual class definition to be available when loading the model.
Exporting Model on ONNX
文档信息
- 本文作者:weownthenight
- 本文链接:https://weownthenight.github.io/2021/05/12/Pytorch%E5%AE%98%E7%BD%91Tutorials%E7%AC%94%E8%AE%B0-%E4%BA%8C/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)