From simple Linear Regression to complicated neural networks
From manual coding gradients to auto gradients
From simple Linear Regression to complicated neural networks
- Pevious: Let the computer fit functions
??? 我们只能让计算机拟合简单的线性函数
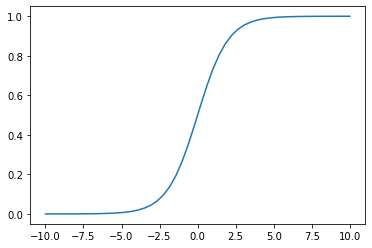
除了线性函数关系(kx+b)还有一种常见的函数关系是“S”型的一种函数
\[sigmoid(x) = \sigma(x) = \frac{1}{1 + e^{(-x)}}\]import numpy as np
import matplotlib.pyplot as plt
import random
def sigmoid(x):
return 1 / (1 + np.exp(-x))
sub_x = np.linspace(-10,10)
plt.plot(sub_x, sigmoid(sub_x))
[<matplotlib.lines.Line2D at 0x7f8adc55a760>]
def random_linear(x):
k, b = random.normalvariate(0,1), random.normalvariate(0,1)
return k*x+b
for _ in range(5):
plt.plot(sub_x,random_linear(sigmoid(random_linear(sub_x))))
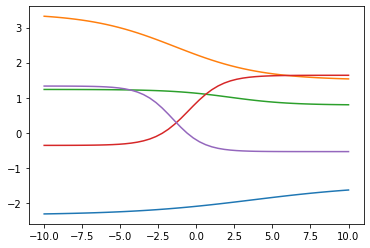
?? 如何拟合众多的复杂函数呢?
发现人类复杂活动的背后是脑内基本神经元的组合,而不是多种多样复杂的神经元。
for _ in range(5):
i = random.choice(range(len(sub_x)))
output1 = np.concatenate((random_linear(sub_x[:i]),random_linear(sub_x[i:])))
plt.plot(sub_x,output1)

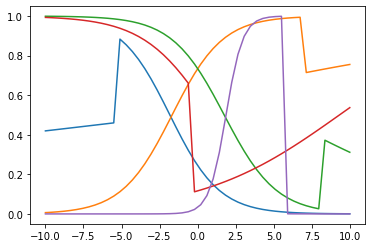
for _ in range(5):
i = random.choice(range(len(sub_x)))
linear_output = np.concatenate((random_linear(sub_x[:i]),random_linear(sub_x[i:])))
i2 = random.choice(range(len(linear_output)))
output = np.concatenate((sigmoid(linear_output[:i2]),sigmoid(linear_output[i2:])))
plt.plot(sub_x,output)
from matplotlib.animation import FuncAnimation
%matplotlib notebook
def draw(index):
i = random.choice(range(len(sub_x)))
linear_output = np.concatenate((random_linear(sub_x[:i]),random_linear(sub_x[i:])))
i2 = random.choice(range(len(linear_output)))
output = np.concatenate((random_linear(sigmoid(linear_output[:i2])),random_linear(sigmoid(linear_output[i2:]))))
fig.clear()
plt.plot(sub_x,output,color = 'green')
fig = plt.gcf()
FuncAnimation(fig,draw,interval=500)
<IPython.core.display.Javascript object>
<matplotlib.animation.FuncAnimation at 0x7f8adcb27c40>
现实中的函数有很多种,每次出现一个情况就需要新构造一个函数太复杂。我们如何用机器自动拟合出更加复杂的函数?就像上面利用两个基本的函数:线性函数和sigmoid,可以拼接组合成复杂的函数。
在大脑中也是一些神经元进行线性变化,一些神经元进行非线性变化,我们把进行非线性变化的神经元称为激活神经元(Active Nuron),在AI中,我们把这种函数(上例中的sigmoid)称为激活函数(Activate Function)。激活函数的作用就是为了让我们的函数能拟合非线性关系。
把这种叫做神经网络,以前科学家们认为神经网络不能超过三层。
做机器学习要注意的点:
- 要有高精度必须要有足够的数据量。
- 在相似的问题下,每当我们需要拟合的参数多一个,需要的数据量要多一个数量级。
当神经网络超过三层时,参数变多了,数据量却没有这么多。
时间到了现在,产生了大量的数据,为神经网络提供了更多的数据资源,层数可以超过三层,我们把层数超过三层的网络称为深度网络。
From manual coding gradients to auto gradients
结合上节课的代码,如果我们把波士顿房价问题也转换为类似的线性和sigmoid的关系,会怎么样呢?
def model(x,k1,b1,k2,b2):
linear1_output = k1 * x + b1
sigmoid_output = sigmoid(linear_output)
linear2_output = k2 * sigmoid_output + b2
return linear2_output
此时发现一个问题:loss函数变得很复杂,这时如何求导呢?
VAR_MAX,VAR_MIN = 100, -100
k, b = random.randint(VAR_MIN,VAR_MAX),random.randint(VAR_MIN,VAR_MAX)
k_b_history = []
total_times = 2000 #总共尝试1000次
min_loss = float('inf') #最好的loss无穷大
best_k,best_b = None, None
alpha = 1e-2
for t in range(total_times):
k1 = k1 + (-1) * loss对k1的偏导 * alpha
b1 = b1 + (-1) * loss对b1的偏导 * alpha
k2 = k2 + (-1) * loss对k2的偏导 * alpha
b2 = b2 + (-1) * loss对b2的偏导 * alpha
loss_ = loss(Y,X_rm*k+b)
if loss_ < min_loss:
min_loss = loss_
best_k, best_b = k,b
k_b_history.append((best_k,best_b))
#print('在{}时刻我找到了更好的k:{}和b:{},这个时候的loss是:{}'.format(t,k,b,loss_))
此时求导可以这样写:$ \displaystyle\frac{\partial loss}{\partial k1} = \frac{\partial loss}{\partial l2}\cdot\frac{\partial l2}{\partial\sigma}\cdot\frac{\partial\sigma}{\partial l1}\cdot\frac{\partial l1}{\partial k1} $ (链式求导)
其中 $ \sigma(x)^{‘} = \sigma(x)(1-\sigma(x)) $
接下来的问题是如何让计算机知道链式求导?自动地求出来?
- Define Problem: Given Model Definition, including the parameters:{k1,k2,b1,b2}, 构建以一个程序,让它能够求解出来k1,k2,b1,b2的偏导是多少。
观察输入输出的关系,可以知道存在:$ k1,b1,x->l1->\sigma,k2,b2->l2,y_{true}->loss $。接下来的问题是:
我们如何用计算机表示上述关系?(数据结构-图)
computing_graph = {
'k1':['L1'],
'b1':['L1'],
'x':['L1'],
'L1':['sigmoid'],
'k2':['L2'],
'b2':['L2'],
'sigmoid':['L2'],
'L2':['Loss'],
'y':['Loss']
}
import networkx as nx
nx.draw(nx.DiGraph(computing_graph), with_labels = True)
Based on the graph representation
如何求出来Loss对k1的偏导?
def get_output(graph,node):
outputs = []
for n, links in graph.items():
if node == n: outputs += links
return outputs
get_output(computing_graph, 'k1')
- 获得k1的输出结点
- 获得k1的输出结点的输出结点
- …直到我们找到了最后一个结点
def get_parameter_partial_order(p):
computing_order = []
target = p
out = get_output(computing_graph,target)[0]
computing_order.append(target)
while out:
computing_order.append(out)
out = get_output(computing_graph,out)
if out:out = out[0]
order = []
for index, n in enumerate(computing_order[:-1]):
order.append((computing_order[index+1],n))
return '*'.join(['∂{}/∂{}'.format(a,b) for a,b in order[::-1]])
for p in ['b1','k1','b2','k2']:
print(get_parameter_partial_order(p))
到这里,我们能够自动地求解各个参数的导数了
如果有一个内存记录结果,我们应该先算$ \frac{\partial Loss}{\partial L2} $和$ \frac{\partial L2}{\partial sigmoid} $和$ \frac{\partial sigmoid}{\partial L1}$然后存放好,可以减少重复计算。
实际这个计算顺序就是图的拓扑排序
Review
- 通过基本的函数我们可以拟合非常复杂的函数
- 什么是激活函数,激活函数的意义和作用是什么
- 什么是神经网络以及它的历史
- 人工智能、神经网络、机器学习、深度学习之间有什么关系
- 链式求导,以及为什么要有链式求导
- 如何让计算机自动求出来求导的顺序,依据我们的模型定义(back propogation)
- 反向传播的意义和作用?
- 为了能够快速求解每个参数的导数需要构建一个图
- 图的拓扑排序的作用
- 图的拓扑排序的实现原理
Next
- 实现拓扑排序
- 把输入、输出、计算、求导每个结点都用到的功能封装成一个类
- 把这些类进行封装,能够自动实现求导,自动实现参数权重的更新(1,2,3)就是一个神经网络框架的核心
- CNN,图像处理,文字处理等和我们的模型是什么关系
- 我们把所学到的东西进行打包,进行通用化,发布到互联网,变成一个通用的人工智能框架。