从零构建深度学习框架（三）

实现拓扑排序

simple_graph={
    'a':[1,2],
    'b':[2,3]
}

list(simple_graph.keys())

['a', 'b']

list(simple_graph.values())

[[1, 2], [2, 3]]

from functools import reduce

reduce(lambda a,b:a+b,list(simple_graph.values()))

[1, 2, 2, 3]

import random

def topologic(graph):
    """graph: dict
    {
        x: [linear],
        k: [linear],
        b: [linear],
        linear: [sigmoid],
        sigmoid:[loss],
        y:[loss],
    }
    """
    
    sorted_node=[]
    
    while graph:
        all_nodes_have_inputs=reduce(lambda a,b:a+b,list(graph.values()))
        all_nodes_have_outputs=list(graph.keys())
        
        all_nodes_only_have_outputs_no_inputs=set(all_nodes_have_outputs)-set(all_nodes_have_inputs)
        
        if all_nodes_only_have_outputs_no_inputs:
            node=random.choice(list(all_nodes_only_have_outputs_no_inputs))
            
            sorted_node.append(node)
            if len(graph)==1: sorted_node+=graph[node]
                
            graph.pop(node)
            
            for _, links in graph.items():
                if node in links: links.remove(node)
        else:
            raise TypeError('this graph has circle, which cannot get topological order')
        
    return sorted_node
    

x,k,b,linear,sigmoid,y,loss='x','k','b','linear','sigmoid','y','loss'

test_graph =  {
        x: [linear],
        k: [linear],
        b: [linear],
        linear: [sigmoid],
        sigmoid:[loss],
        y:[loss],
}

import networkx as nx

nx.draw(nx.DiGraph(test_graph), with_labels = True)

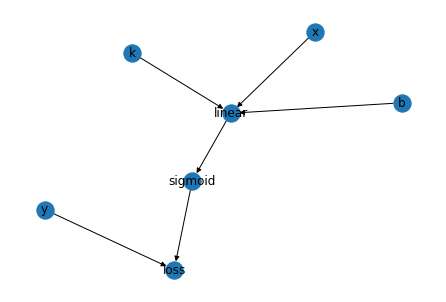
png01

topologic(test_graph)

['k', 'y', 'b', 'x', 'linear', 'sigmoid', 'loss']

写代码的一个理念：Code Self-Description Good Documents!==> The best document is the source code

一起来见证拓扑排序的威力吧！！！

import numpy as np

class Node:
    def __init__(self, inputs=[],name=None,is_trainable=False):
        self.inputs=inputs
        self.outputs=[]
        self.name=name
        self.value=None
        self.gradients=dict()  #存储loss对某个值的偏导
        self.is_trainable=is_trainable
        
        for node in inputs:
            node.outputs.append(self)
      
    def backward(self):
        pass
    
    def forward(self):
       # print('I am {}, I calculate myself value by myself!!!'.format(self.name))
        pass
    
    def __repr__(self):
        return 'Node: {}'.format(self.name)  

class Placeholder(Node):
    def __init__(self, name=None,is_trainable=False):
        Node.__init__(self,name=name,is_trainable=is_trainable)
    
    def __repr__(self):
        return 'Placeholder: {}'.format(self.name)
    
   # def forward(self):
   #     print('I am {}, I was assigned value: {} by human!!!'.format(self.name,self.value))
    
    def backward(self):
        self.gradients[self]=self.outputs[0].gradients[self]
        
class Linear(Node):
    def __init__(self,x,k,b,name=None):
        Node.__init__(self, inputs=[x,k,b],name=name)
    
    def __repr__(self):
        return 'Linear: {}'.format(self.name)
    
    def forward(self):
        
        x,k,b=self.inputs[0],self.inputs[1],self.inputs[2]
        
        self.value=k.value*x.value+b.value
       # print('I am {}, I calculate myself value: {} by myself!!!'.format(self.name,self.value))
    
    def backward(self):
        x,k,b=self.inputs[0],self.inputs[1],self.inputs[2]
        self.gradients[self.inputs[0]]=self.outputs[0].gradients[self]*k.value
        self.gradients[self.inputs[1]]=self.outputs[0].gradients[self]*x.value
        self.gradients[self.inputs[2]]=self.outputs[0].gradients[self]*1
        
        #print('self.gradients[self.inputs[0]]| {}'.format(self.gradients[self.inputs[0]]))
        #print('self.gradients[self.inputs[1]]| {}'.format(self.gradients[self.inputs[1]]))
        #print('self.gradients[self.inputs[2]]| {}'.format(self.gradients[self.inputs[2]]))
        
class Sigmoid(Node):
    def __init__(self,x,name=None):
        Node.__init__(self, inputs=[x],name=name)
    
    def _sigmoid(self,x):
        return 1 / (1 + np.exp((-1)*x))
    
    def __repr__(self):
        return 'Sigmoid: {}'.format(self.name)
    
    def forward(self):
        x=self.inputs[0]
        
        self.value=self._sigmoid(x.value)
        #print('I am {}, I calculate myself value: {} by myself!!!'.format(self.name,self.value))
    
    def backward(self):
        x=self.inputs[0]
        self.gradients[self.inputs[0]]=self.outputs[0].gradients[self]*(self._sigmoid(x.value)*(1-self._sigmoid(x.value)))
        #print('self.gradients[self.inputs[0]]| {}'.format(self.gradients[self.inputs[0]]))
        
class Loss(Node):
    def __init__(self,y,yhat,name=None):
        Node.__init__(self, inputs=[y,yhat],name=name)
    
    def __repr__(self):
        return 'Loss: {}'.format(self.name)
    
    def forward(self):
        y,yhat=self.inputs[0],self.inputs[1]
        
        self.value=np.mean((y.value-yhat.value)**2)
        #print('I am {}, I calculate myself value: {} by myself!!!'.format(self.name,self.value))
    
    def backward(self):
        y=self.inputs[0]
        yhat=self.inputs[1]
        self.gradients[self.inputs[0]]=2*np.mean(y.value-yhat.value)
        self.gradients[self.inputs[1]]=-2*np.mean(y.value-yhat.value)
        #print('self.gradients[self.inputs[0]].{} | {}'.format(self.inputs[0].name,self.gradients[self.inputs[0]]))
        #print('self.gradients[self.inputs[1]].{} | {}'.format(self.inputs[0].name,self.gradients[self.inputs[1]]))
      
## Our Simple Model Elements

node_x = Placeholder(name='x')
node_y = Placeholder(name='y')
node_k = Placeholder(name='k',is_trainable=True)
node_b = Placeholder(name='b',is_trainable=True)
node_linear = Linear(x=node_x,k=node_k,b=node_b,name='linear')
node_sigmoid = Sigmoid(x=node_linear,name='sigmoid')
node_loss = Loss(yhat=node_sigmoid, y=node_y,name='loss')

##告诉一个结点的输入的同时也相当于告诉了另一个结点的输出,所以可以简化为无需输出

如何建图？

通过外围的结点扩充生成连接图。外围的结点就是指那些没有输入的结点。

feed_dict={
    node_x:3,
    node_y:random.random(),
    node_k:random.random(),
    node_b:0.38
    
}

from collections import defaultdict

def convert_feed_dict_to_graph(feed_dict):
    need_expand = [n for n in feed_dict]
    computing_graph = defaultdict(list)

    while need_expand:
        n = need_expand.pop(0)
    
        if n in computing_graph: continue
            
        if isinstance(n,Placeholder): n.value = feed_dict[n]
        
        for m in n.outputs:
            computing_graph[n].append(m)
            need_expand.append(m)
    return computing_graph

sorted_nodes=topologic(convert_feed_dict_to_graph(feed_dict))

sorted_nodes

[Placeholder: k,
 Placeholder: x,
 Placeholder: b,
 Linear: linear,
 Sigmoid: sigmoid,
 Placeholder: y,
 Loss: loss]

模拟神经网络的计算过程

## FeedForward

def forward(graph_sorted_nodes):
    for node in sorted_nodes:
        node.forward()
        if isinstance(node,Loss):
            print('loss value:{}'.format(node.value))
    
## Backward Propogation(反向传播)

def backward(graph_sorted_nodes):
    for node in sorted_nodes[::-1]:
        #print('I am: {}'.format(node.name))
        node.backward()
    
def run_one_epoch(graph_sorted_nodes):
    forward(graph_sorted_nodes)
    backward(graph_sorted_nodes)

##optimize

def optimize(graph_nodes,learning_rate=1e-3):
    for node in graph_nodes:
        if node.is_trainable:
            node.value=node.value-1*node.gradients[node]*learning_rate
            cmp='large' if node.gradients[node]>0 else 'small'
            print("{}' value is too {}, I need update myself to {}".format(node.name,cmp,node.value))
     

经过拓扑排序可以保证后续结点一定在后续计算

完整的一次求值-求导-更新应该是：

loss_history=[]
for _ in range(100):
    run_one_epoch(sorted_nodes)
    __loss_node=sorted_nodes[-1]
    assert isinstance(__loss_node, Loss)
    
    loss_history.append(__loss_node.value)
    optimize(sorted_nodes,learning_rate=1e-1)

loss value:0.0002993652115879464
k' value is too large, I need update myself to 0.7055159216563167
b' value is too large, I need update myself to 0.3797571499089143
loss value:0.00029349062436637613
k' value is too large, I need update myself to 0.7047930681691197
b' value is too large, I need update myself to 0.37951619874651527
loss value:0.00028770771576464547
k' value is too large, I need update myself to 0.7040759084732403
b' value is too large, I need update myself to 0.3792771455145555
loss value:0.00028201571407244694
k' value is too large, I need update myself to 0.7033644388015124
b' value is too large, I need update myself to 0.37903998895731283
loss value:0.0002764138366269794
k' value is too large, I need update myself to 0.7026586546208644
b' value is too large, I need update myself to 0.3788047275637635
loss value:0.00027090129030499157
k' value is too large, I need update myself to 0.7019585506391256
b' value is too large, I need update myself to 0.37857135956985055
loss value:0.000265477272014349
k' value is too large, I need update myself to 0.7012641208121136
b' value is too large, I need update myself to 0.3783398829608466
loss value:0.00026014096918464585
k' value is too large, I need update myself to 0.7005753583509948
b' value is too large, I need update myself to 0.378110295473807
loss value:0.0002548915602565695
k' value is too large, I need update myself to 0.6998922557299108
b' value is too large, I need update myself to 0.37788259460011225
loss value:0.000249728215169412
k' value is too large, I need update myself to 0.6992148046938623
b' value is too large, I need update myself to 0.37765677758809607
loss value:0.00024465009584641475
k' value is too large, I need update myself to 0.6985429962668447
b' value is too large, I need update myself to 0.37743284144575684
loss value:0.00023965635667751314
k' value is too large, I need update myself to 0.6978768207602243
b' value is too large, I need update myself to 0.37721078294355004
loss value:0.00023474614499911024
k' value is too large, I need update myself to 0.6972162677813498
b' value is too large, I need update myself to 0.37699059861725853
loss value:0.0002299186015703887
k' value is too large, I need update myself to 0.6965613262423892
b' value is too large, I need update myself to 0.3767722847709383
loss value:0.0002251728610459471
k' value is too large, I need update myself to 0.6959119843693843
b' value is too large, I need update myself to 0.3765558374799367
loss value:0.000220508052444231
k' value is too large, I need update myself to 0.6952682297115148
b' value is too large, I need update myself to 0.3763412525939802
loss value:0.00021592329961154185
k' value is too large, I need update myself to 0.6946300491505627
b' value is too large, I need update myself to 0.3761285257403295
loss value:0.0002114177216811902
k' value is too large, I need update myself to 0.6939974289105691
b' value is too large, I need update myself to 0.3759176523269983
loss value:0.00020699043352749209
k' value is too large, I need update myself to 0.6933703545676749
b' value is too large, I need update myself to 0.37570862754603357
loss value:0.00020264054621435142
k' value is too large, I need update myself to 0.6927488110601354
b' value is too large, I need update myself to 0.37550144637685373
loss value:0.00019836716743800375
k' value is too large, I need update myself to 0.6921327826985028
b' value is too large, I need update myself to 0.3752961035896428
loss value:0.00019416940196377575
k' value is too large, I need update myself to 0.6915222531759645
b' value is too large, I need update myself to 0.3750925937487967
loss value:0.00019004635205646154
k' value is too large, I need update myself to 0.6909172055788321
b' value is too large, I need update myself to 0.3748909112164192
loss value:0.0001859971179041359
k' value is too large, I need update myself to 0.6903176223971689
b' value is too large, I need update myself to 0.37469105015586485
loss value:0.00018202079803512507
k' value is too large, I need update myself to 0.6897234855355504
b' value is too large, I need update myself to 0.37449300453532536
loss value:0.00017811648972788048
k' value is too large, I need update myself to 0.6891347763239464
b' value is too large, I need update myself to 0.37429676813145735
loss value:0.00017428328941360675
k' value is too large, I need update myself to 0.6885514755287179
b' value is too large, I need update myself to 0.37410233453304786
loss value:0.00017052029307131742
k' value is too large, I need update myself to 0.6879735633637198
b' value is too large, I need update myself to 0.3739096971447152
loss value:0.00016682659661527137
k' value is too large, I need update myself to 0.6874010195015003
b' value is too large, I need update myself to 0.3737188491906421
loss value:0.0001632012962744753
k' value is too large, I need update myself to 0.6868338230845885
b' value is too large, I need update myself to 0.3735297837183381
loss value:0.00015964348896416658
k' value is too large, I need update myself to 0.6862719527368629
b' value is too large, I need update myself to 0.3733424936024296
loss value:0.00015615227264910856
k' value is too large, I need update myself to 0.6857153865749913
b' value is too large, I need update myself to 0.3731569715484724
loss value:0.00015272674669856566
k' value is too large, I need update myself to 0.6851641022199338
b' value is too large, I need update myself to 0.3729732100967865
loss value:0.0001493660122327569
k' value is too large, I need update myself to 0.684618076808502
b' value is too large, I need update myself to 0.37279120162630924
loss value:0.0001460691724608083
k' value is too large, I need update myself to 0.6840772870049644
b' value is too large, I need update myself to 0.3726109383584634
loss value:0.00014283533301001926
k' value is too large, I need update myself to 0.6835417090126922
b' value is too large, I need update myself to 0.3724324123610393
loss value:0.0001396636022463227
k' value is too large, I need update myself to 0.6830113185858353
b' value is too large, I need update myself to 0.372255615552087
loss value:0.00013655309158595928
k' value is too large, I need update myself to 0.6824860910410229
b' value is too large, I need update myself to 0.3720805397038162
loss value:0.00013350291579825106
k' value is too large, I need update myself to 0.6819660012690796
b' value is too large, I need update myself to 0.3719071764465018
loss value:0.00013051219329938255
k' value is too large, I need update myself to 0.6814510237467504
b' value is too large, I need update myself to 0.37173551727239207
loss value:0.00012758004643726147
k' value is too large, I need update myself to 0.6809411325484265
b' value is too large, I need update myself to 0.3715655535396174
loss value:0.00012470560176730913
k' value is too large, I need update myself to 0.6804363013578654
b' value is too large, I need update myself to 0.37139727647609705
loss value:0.00012188799031925642
k' value is too large, I need update myself to 0.679936503479898
b' value is too large, I need update myself to 0.37123067718344127
loss value:0.00011912634785487527
k' value is too large, I need update myself to 0.6794417118521153
b' value is too large, I need update myself to 0.37106574664084707
loss value:0.00011641981511671455
k' value is too large, I need update myself to 0.6789518990565289
b' value is too large, I need update myself to 0.37090247570898494
loss value:0.00011376753806778417
k' value is too large, I need update myself to 0.6784670373311975
b' value is too large, I need update myself to 0.37074085513387445
loss value:0.00011116866812227805
k' value is too large, I need update myself to 0.6779870985818144
b' value is too large, I need update myself to 0.37058087555074676
loss value:0.0001086223623673184
k' value is too large, I need update myself to 0.6775120543932484
b' value is too large, I need update myself to 0.37042252748789145
loss value:0.00010612778377582732
k' value is too large, I need update myself to 0.6770418760410328
b' value is too large, I need update myself to 0.37026580137048626
loss value:0.00010368410141048298
k' value is too large, I need update myself to 0.6765765345027965
b' value is too large, I need update myself to 0.3701106875244075
loss value:0.00010129049061895284
k' value is too large, I need update myself to 0.6761160004696309
b' value is too large, I need update myself to 0.369957176180019
loss value:9.894613322032313e-05
k' value is too large, I need update myself to 0.6756602443573878
b' value is too large, I need update myself to 0.36980525747593795
loss value:9.665021768294997e-05
k' value is too large, I need update myself to 0.6752092363179023
b' value is too large, I need update myself to 0.3696549214627761
loss value:9.440193929371623e-05
k' value is too large, I need update myself to 0.6747629462501359
b' value is too large, I need update myself to 0.369506158106854
loss value:9.220050031878914e-05
k' value is too large, I need update myself to 0.6743213438112347
b' value is too large, I need update myself to 0.3693589572938869
loss value:9.004511015608518e-05
k' value is too large, I need update myself to 0.6738843984274973
b' value is too large, I need update myself to 0.3692133088326411
loss value:8.793498547937345e-05
k' value is too large, I need update myself to 0.6734520793052485
b' value is too large, I need update myself to 0.3690692024585582
loss value:8.586935037431183e-05
k' value is too large, I need update myself to 0.6730243554416142
b' value is too large, I need update myself to 0.36892662783734675
loss value:8.384743646638239e-05
k' value is too large, I need update myself to 0.6726011956351923
b' value is too large, I need update myself to 0.36878557456853944
loss value:8.186848304093888e-05
k' value is too large, I need update myself to 0.6721825684966168
b' value is too large, I need update myself to 0.36864603218901426
loss value:7.993173715547642e-05
k' value is too large, I need update myself to 0.6717684424590105
b' value is too large, I need update myself to 0.3685079901764788
loss value:7.803645374421818e-05
k' value is too large, I need update myself to 0.6713587857883218
b' value is too large, I need update myself to 0.3683714379529159
loss value:7.618189571520533e-05
k' value is too large, I need update myself to 0.6709535665935438
b' value is too large, I need update myself to 0.3682363648879899
loss value:7.436733404000056e-05
k' value is too large, I need update myself to 0.6705527528368108
b' value is too large, I need update myself to 0.36810276030241224
loss value:7.259204783614897e-05
k' value is too large, I need update myself to 0.6701563123433695
b' value is too large, I need update myself to 0.36797061347126514
loss value:7.085532444257293e-05
k' value is too large, I need update myself to 0.6697642128114214
b' value is too large, I need update myself to 0.36783991362728247
loss value:6.915645948799663e-05
k' value is too large, I need update myself to 0.669376421821835
b' value is too large, I need update myself to 0.367710649964087
loss value:6.749475695261497e-05
k' value is too large, I need update myself to 0.6689929068477231
b' value is too large, I need update myself to 0.367582811639383
loss value:6.586952922311707e-05
k' value is too large, I need update myself to 0.6686136352638841
b' value is too large, I need update myself to 0.36745638777810335
loss value:6.428009714123249e-05
k' value is too large, I need update myself to 0.6682385743561042
b' value is too large, I need update myself to 0.3673313674755101
loss value:6.272579004598307e-05
k' value is too large, I need update myself to 0.6678676913303192
b' value is too large, I need update myself to 0.36720773980024846
loss value:6.120594580976506e-05
k' value is too large, I need update myself to 0.6675009533216323
b' value is too large, I need update myself to 0.36708549379735284
loss value:5.9719910868426904e-05
k' value is too large, I need update myself to 0.6671383274031879
b' value is too large, I need update myself to 0.3669646184912047
loss value:5.8267040245557534e-05
k' value is too large, I need update myself to 0.6667797805948984
b' value is too large, I need update myself to 0.3668451028884415
loss value:5.684669757106046e-05
k' value is too large, I need update myself to 0.6664252798720227
b' value is too large, I need update myself to 0.3667269359808163
loss value:5.5458255094257576e-05
k' value is too large, I need update myself to 0.6660747921735957
b' value is too large, I need update myself to 0.36661010674800726
loss value:5.410109369163729e-05
k' value is too large, I need update myself to 0.6657282844107063
b' value is too large, I need update myself to 0.3664946041603775
loss value:5.277460286944297e-05
k' value is too large, I need update myself to 0.6653857234746243
b' value is too large, I need update myself to 0.36638041718168346
loss value:5.1478180761226595e-05
k' value is too large, I need update myself to 0.6650470762447738
b' value is too large, I need update myself to 0.36626753477173324
loss value:5.021123412057662e-05
k' value is too large, I need update myself to 0.6647123095965529
b' value is too large, I need update myself to 0.366155945888993
loss value:4.8973178309131945e-05
k' value is too large, I need update myself to 0.6643813904090002
b' value is too large, I need update myself to 0.36604563949314206
loss value:4.776343728011335e-05
k' value is too large, I need update myself to 0.6640542855723047
b' value is too large, I need update myself to 0.36593660454757687
loss value:4.658144355744394e-05
k' value is too large, I need update myself to 0.6637309619951616
b' value is too large, I need update myself to 0.3658288300218625
loss value:4.542663821068787e-05
k' value is too large, I need update myself to 0.6634113866119722
b' value is too large, I need update myself to 0.3657223048941327
loss value:4.429847082595706e-05
k' value is too large, I need update myself to 0.6630955263898879
b' value is too large, I need update myself to 0.36561701815343794
loss value:4.3196399472891484e-05
k' value is too large, I need update myself to 0.6627833483356986
b' value is too large, I need update myself to 0.36551295880204154
loss value:4.211989066792699e-05
k' value is too large, I need update myself to 0.6624748195025653
b' value is too large, I need update myself to 0.36541011585766375
loss value:4.1068419333987564e-05
k' value is too large, I need update myself to 0.6621699069965966
b' value is too large, I need update myself to 0.3653084783556742
loss value:4.004146875671875e-05
k' value is too large, I need update myself to 0.6618685779832711
b' value is too large, I need update myself to 0.36520803535123236
loss value:3.903853053747362e-05
k' value is too large, I need update myself to 0.6615707996937038
b' value is too large, I need update myself to 0.3651087759213766
loss value:3.805910454312546e-05
k' value is too large, I need update myself to 0.6612765394307583
b' value is too large, I need update myself to 0.3650106891670614
loss value:3.7102698852931306e-05
k' value is too large, I need update myself to 0.6609857645750058
b' value is too large, I need update myself to 0.36491376421514393
loss value:3.616882970250796e-05
k' value is too large, I need update myself to 0.6606984425905306
b' value is too large, I need update myself to 0.36481799022031886
loss value:3.525702142512383e-05
k' value is too large, I need update myself to 0.6604145410305826
b' value is too large, I need update myself to 0.36472335636700287
loss value:3.436680639041629e-05
k' value is too large, I need update myself to 0.6601340275430796
b' value is too large, I need update myself to 0.36462985187116853
loss value:3.349772494066317e-05
k' value is too large, I need update myself to 0.6598568698759579
b' value is too large, I need update myself to 0.36453746598212794
loss value:3.2649325324769834e-05
k' value is too large, I need update myself to 0.659583035882374
b' value is too large, I need update myself to 0.3644461879842666
loss value:3.1821163630050975e-05
k' value is too large, I need update myself to 0.6593124935257574
b' value is too large, I need update myself to 0.36435600719872774
loss value:3.1012803711996946e-05
k' value is too large, I need update myself to 0.6590452108847167
b' value is too large, I need update myself to 0.3642669129850475
loss value:3.022381712209968e-05
k' value is too large, I need update myself to 0.6587811561577991
b' value is too large, I need update myself to 0.3641788947427416

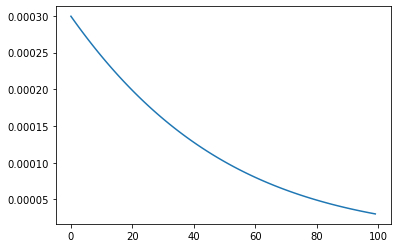
import matplotlib.pyplot as plt

plt.plot(loss_history)

[<matplotlib.lines.Line2D at 0x7f8d58f36130>]

png02

sorted_nodes

[Placeholder: k,
 Placeholder: x,
 Placeholder: b,
 Linear: linear,
 Sigmoid: sigmoid,
 Placeholder: y,
 Loss: loss]

def sigmoid(x):
    return 1 / ( 1 + np.exp(-x))

sigmoid(sorted_nodes[3].value*sorted_nodes[0].value+sorted_nodes[1].value)   #sigmoid(kx+b)

0.9894651097672786

sorted_nodes[2].value    #y

0.3641788947427416

其实，我们不经意间，已经完成了深度学习框架的核心内容了！！！

如何处理多维数据？

现在看到的结果自变量x，y是一维的，如何处理多维数据呢？

多维数组的写法和上述几乎完全一样，以波士顿房价为例，只讲一下不同的地方：

import numpy as np
import random

class Node:
    def __init__(self, inputs=[]):
        self.inputs = inputs
        self.outputs = []

        for n in self.inputs:
            n.outputs.append(self)
            # set 'self' node as inbound_nodes's outbound_nodes

        self.value = None

        self.gradients = {}
        # keys are the inputs to this node, and their
        # values are the partials of this node with 
        # respect to that input.
        # \partial{node}{input_i}
        

    def forward(self):
        '''
        Forward propagation. 
        Compute the output value vased on 'inbound_nodes' and store the 
        result in self.value
        '''

        raise NotImplemented
    

    def backward(self):

        raise NotImplemented
        
class Placeholder(Node):
    def __init__(self):
        '''
        An Input node has no inbound nodes.
        So no need to pass anything to the Node instantiator.
        '''
        Node.__init__(self)

    def forward(self, value=None):
        '''
        Only input node is the node where the value may be passed
        as an argument to forward().
        All other node implementations should get the value of the 
        previous node from self.inbound_nodes
        
        Example: 
        val0: self.inbound_nodes[0].value
        '''
        if value is not None:
            self.value = value
            ## It's is input node, when need to forward, this node initiate self's value.

        # Input subclass just holds a value, such as a data feature or a model parameter(weight/bias)
        
    def backward(self):
        self.gradients = {self:0}
        for n in self.outputs:
            grad_cost = n.gradients[self]
            self.gradients[self] = grad_cost * 1
            
        
        # input N --> N1, N2
        # \partial L / \partial N 
        # ==> \partial L / \partial N1 * \ partial N1 / \partial N


class Add(Node):
    def __init__(self, *nodes):
        Node.__init__(self, nodes)


    def forward(self):
        self.value = sum(map(lambda n: n.value, self.inputs))
        ## when execute forward, this node caculate value as defined.

class Linear(Node):
    def __init__(self, nodes, weights, bias):
        Node.__init__(self, [nodes, weights, bias])

    def forward(self):
        inputs = self.inputs[0].value
        weights = self.inputs[1].value
        bias = self.inputs[2].value

        self.value = np.dot(inputs, weights) + bias
        
    def backward(self):

        # initial a partial for each of the inbound_nodes.
        #单个变量的版本默认gradients是0，多维变量则要定义为零矩阵
        self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}

        for n in self.outputs:
            # Get the partial of the cost w.r.t this node.
            grad_cost = n.gradients[self]
            
            #不同于单个变量的版本，多维变量进行求导需要矩阵运算点承
            self.gradients[self.inputs[0]] = np.dot(grad_cost, self.inputs[1].value.T)
            self.gradients[self.inputs[1]] = np.dot(self.inputs[0].value.T, grad_cost)
            self.gradients[self.inputs[2]] = np.sum(grad_cost, axis=0, keepdims=False)

        # WX + B / W ==> X
        # WX + B / X ==> W

class Sigmoid(Node):
    def __init__(self, node):
        Node.__init__(self, [node])


    def _sigmoid(self, x):
        return 1./(1 + np.exp(-1 * x))

    def forward(self):
        self.x = self.inputs[0].value
        self.value = self._sigmoid(self.x)

    def backward(self):
        self.partial = self._sigmoid(self.x) * (1 - self._sigmoid(self.x))
        
        # y = 1 / (1 + e^-x)
        # y' = 1 / (1 + e^-x) (1 - 1 / (1 + e^-x))
        
        self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}

        for n in self.outputs:
            grad_cost = n.gradients[self]  # Get the partial of the cost with respect to this node.

            self.gradients[self.inputs[0]] = grad_cost * self.partial
            # use * to keep all the dimension same!.



class MSE(Node):
    def __init__(self, y, a):
        Node.__init__(self, [y, a])


    def forward(self):
        y = self.inputs[0].value.reshape(-1, 1)
        a = self.inputs[1].value.reshape(-1, 1)
        assert(y.shape == a.shape)

        self.m = self.inputs[0].value.shape[0]
        self.diff = y - a

        self.value = np.mean(self.diff**2)


    def backward(self):
        self.gradients[self.inputs[0]] = (2 / self.m) * self.diff
        self.gradients[self.inputs[1]] = (-2 / self.m) * self.diff


def forward_and_backward(graph):
    # execute all the forward method of sorted_nodes.

    ## In practice, it's common to feed in mutiple data example in each forward pass rather than just 1. Because the examples can be processed in parallel. The number of examples is called batch size.
    for n in graph:
        n.forward()
        ## each node execute forward, get self.value based on the topological sort result.

    for n in  graph[::-1]:
        n.backward()

###   v -->  a -->  C
##    b --> C
##    b --> v -- a --> C
##    v --> v ---> a -- > C

def toplogic(graph):
    sorted_node = []
    
    while len(graph) > 0: 

        all_inputs = []
        all_outputs = []
        
        for n in graph:
            all_inputs += graph[n]
            all_outputs.append(n)
        
        all_inputs = set(all_inputs)
        all_outputs = set(all_outputs)
    
        need_remove = all_outputs - all_inputs  # which in all_inputs but not in all_outputs
    
        if len(need_remove) > 0: 
            node = random.choice(list(need_remove))

            need_to_visited = [node]

            if len(graph) == 1: need_to_visited += graph[node]
                
            graph.pop(node)
            sorted_node += need_to_visited
        
            for _, links in graph.items():
                if node in links: links.remove(node)
        else: # have cycle
            break
        
    return sorted_node

from collections import defaultdict


def convert_feed_dict_to_graph(feed_dict):
    computing_graph = defaultdict(list)
    
    nodes = [n for n in feed_dict]
    
    while nodes:
        n = nodes.pop(0) 
        
        if isinstance(n, Placeholder):
            n.value = feed_dict[n]
        
        if n in computing_graph: continue

        for m in n.outputs:
            computing_graph[n].append(m)
            nodes.append(m)
    
    return computing_graph

def topological_sort_feed_dict(feed_dict):
    graph = convert_feed_dict_to_graph(feed_dict)
    
    return toplogic(graph)


def optimize(trainables, learning_rate=1e-2):
    # there are so many other update / optimization methods
    # such as Adam, Mom, 
    for t in trainables:
        t.value += -1 * learning_rate * t.gradients[t]

boston_graph={
    'x':['l1'],
    'w1':['l1'],
    'b1':['l1'],
    'l1':['s1'],
    's1':['l2'],
    'l2':['cost']
}

nx.draw(nx.DiGraph(boston_graph), with_labels = True)

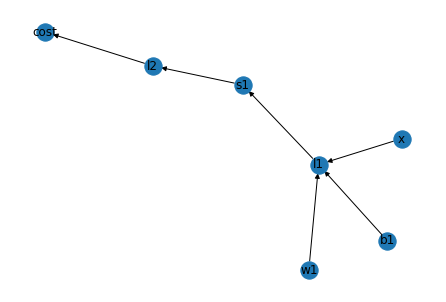
png03

那么多维向量版本能出现什么样的结果呢？

import numpy as np
from sklearn.datasets import load_boston
from sklearn.utils import shuffle, resample
#from miniflow import *

# Load data
data = load_boston()
X_ = data['data']
y_ = data['target']

# Normalize data
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)

n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)

# Neural network
X, y = Placeholder(), Placeholder()
W1, b1 = Placeholder(), Placeholder()
W2, b2 = Placeholder(), Placeholder()

l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)

feed_dict = {
    X: X_,
    y: y_,
    W1: W1_,
    b1: b1_,
    W2: W2_,
    b2: b2_
}

epochs = 5000
# Total number of examples
m = X_.shape[0]
batch_size = 16
steps_per_epoch = m // batch_size

graph = topological_sort_feed_dict(feed_dict)
trainables = [W1, b1, W2, b2]

print("Total number of examples = {}".format(m))

Total number of examples = 506

losses = []

for i in range(epochs):
    loss = 0
    for j in range(steps_per_epoch):
        # Step 1
        # Randomly sample a batch of examples
        X_batch, y_batch = resample(X_, y_, n_samples=batch_size)

        # Reset value of X and y Inputs
        X.value = X_batch
        y.value = y_batch

        # Step 2
        _ = None
        forward_and_backward(graph) # set output node not important.

        # Step 3
        rate = 1e-2
    
        optimize(trainables, rate)

        loss += graph[-1].value
    
    if i % 100 == 0: 
        print("Epoch: {}, Loss: {:.3f}".format(i+1, loss/steps_per_epoch))
        losses.append(loss/steps_per_epoch)

Epoch: 1, Loss: 193.239
Epoch: 101, Loss: 6.906
Epoch: 201, Loss: 5.198
Epoch: 301, Loss: 4.318
Epoch: 401, Loss: 4.248
Epoch: 501, Loss: 3.841
Epoch: 601, Loss: 3.862
Epoch: 701, Loss: 3.452
Epoch: 801, Loss: 3.402
Epoch: 901, Loss: 3.746
Epoch: 1001, Loss: 3.778
Epoch: 1101, Loss: 3.476
Epoch: 1201, Loss: 3.824
Epoch: 1301, Loss: 3.189
Epoch: 1401, Loss: 3.454
Epoch: 1501, Loss: 3.641
Epoch: 1601, Loss: 3.470
Epoch: 1701, Loss: 3.131
Epoch: 1801, Loss: 3.255
Epoch: 1901, Loss: 3.087
Epoch: 2001, Loss: 3.266
Epoch: 2101, Loss: 3.164
Epoch: 2201, Loss: 3.274
Epoch: 2301, Loss: 2.864
Epoch: 2401, Loss: 3.478
Epoch: 2501, Loss: 2.805
Epoch: 2601, Loss: 3.092
Epoch: 2701, Loss: 2.697
Epoch: 2801, Loss: 2.848
Epoch: 2901, Loss: 3.324
Epoch: 3001, Loss: 3.090
Epoch: 3101, Loss: 2.809
Epoch: 3201, Loss: 2.961
Epoch: 3301, Loss: 3.256
Epoch: 3401, Loss: 3.035
Epoch: 3501, Loss: 2.831
Epoch: 3601, Loss: 3.115
Epoch: 3701, Loss: 2.688
Epoch: 3801, Loss: 2.743
Epoch: 3901, Loss: 3.293
Epoch: 4001, Loss: 2.557
Epoch: 4101, Loss: 2.918
Epoch: 4201, Loss: 2.909
Epoch: 4301, Loss: 2.886
Epoch: 4401, Loss: 3.029
Epoch: 4501, Loss: 2.846
Epoch: 4601, Loss: 2.678
Epoch: 4701, Loss: 3.003
Epoch: 4801, Loss: 3.021
Epoch: 4901, Loss: 2.963

如何可视化拟合函数？

效果很好，但是我们想知道到底拟合出来了什么函数怎么办呢？

把维度降低成三维空间就可以看出了

load_boston()['feature_names']

array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
       'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')

原本的波士顿数据集有15个维度，在第一节课我们讲到其中RM和LSTAT是最重要的两个变量，为了看清楚函数，我们只取这两个变量，以此对上面的代码进行修改：

import pandas as pd

import numpy as np
from sklearn.datasets import load_boston
from sklearn.utils import shuffle, resample
#from miniflow import *

#修改X_
# Load data
data = load_boston()
dataframe = pd.DataFrame(data['data'])
dataframe.columns = data['feature_names']

X_ = dataframe[['RM','LSTAT']]
y_ = data['target']

# Normalize data
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)

n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)

# Neural network
X, y = Placeholder(), Placeholder()
W1, b1 = Placeholder(), Placeholder()
W2, b2 = Placeholder(), Placeholder()

l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)

feed_dict = {
    X: X_,
    y: y_,
    W1: W1_,
    b1: b1_,
    W2: W2_,
    b2: b2_
}

epochs = 200
# Total number of examples
m = X_.shape[0]
batch_size = 1
steps_per_epoch = m // batch_size

graph = topological_sort_feed_dict(feed_dict)
trainables = [W1, b1, W2, b2]

print("Total number of examples = {}".format(m))

Total number of examples = 506

修改完后接下来的运行一样：

from tqdm import tqdm_notebook #加个进度条

losses = []

for i in tqdm_notebook(range(epochs)):
    loss = 0
    for j in range(steps_per_epoch):
        # Step 1
        # Randomly sample a batch of examples
        X_batch, y_batch = resample(X_, y_, n_samples=batch_size)

        # Reset value of X and y Inputs
        X.value = X_batch
        y.value = y_batch

        # Step 2
        _ = None
        forward_and_backward(graph) # set output node not important.

        # Step 3
        rate = 1e-2
    
        optimize(trainables, rate)

        loss += graph[-1].value
    
    if i % 100 == 0: 
        print("Epoch: {}, Loss: {:.3f}".format(i+1, loss/steps_per_epoch))
        losses.append(loss/steps_per_epoch)

<ipython-input-36-19371b6a8d01>:3: TqdmDeprecationWarning: This function will be removed in tqdm==5.0.0
Please use `tqdm.notebook.tqdm` instead of `tqdm.tqdm_notebook`
  for i in tqdm_notebook(range(epochs)):

  0%|          | 0/200 [00:00<?, ?it/s]

Epoch: 1, Loss: 38.509
Epoch: 101, Loss: 19.463

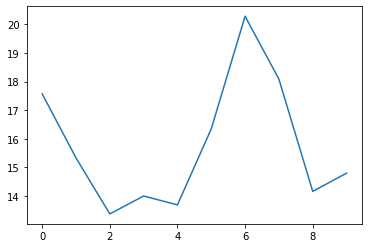
因为维度变少，下降的速度相比之前更慢，但也比第一天40多的loss要准确很多。

plt.plot(losses)

[<matplotlib.lines.Line2D at 0x7f9e2a069400>]

png04

from mpl_toolkits.mplot3d import Axes3D  #三维作图工具

graph

[<__main__.Placeholder at 0x7f9e2b4e3520>,
 <__main__.Placeholder at 0x7f9e2b5511c0>,
 <__main__.Placeholder at 0x7f9e29f5b4f0>,
 <__main__.Placeholder at 0x7f9e2b546820>,
 <__main__.Placeholder at 0x7f9e2b4e34c0>,
 <__main__.Placeholder at 0x7f9e2b4e30a0>,
 <__main__.Linear at 0x7f9e2b5467f0>,
 <__main__.Sigmoid at 0x7f9e2b5465b0>,
 <__main__.Linear at 0x7f9e2b546700>,
 <__main__.MSE at 0x7f9e2b546b50>]

predicate_results = []
for rm, ls in X_.values:
    X.value = np.array([[rm,ls]])
    forward_and_backward(graph)
    predicate_results.append(graph[-2].value[0][0])

predicate_results

[26.931256990280755,
18040855400208,
6966808790294,
71769596618556,
73197046170386,
265277615293396,
900580837120124,
34631708994251,
027595543297709,
204299466704523,
271326965986063,
267085902656945,
036473715959893,
81738095109712,
140244093243215,
56891745536901,
217982877947332,
527761756656695,
078163879190164,
949830730636997,
044117760282766,
87942290293472,
753647948237944,
784104316671428,
73524218999864,
624260891255318,
37621406858645,
062327807717686,
322137840475285,
599252343758465,
41922655859802,
58396220830317,
035233840188434,
188091186490382,
38966292607516,
092513145962332,
220138537762217,
44952696943384,
854559123508515,
17527630830187,
89465679210451,
096209997479146,
58670750239904,
225411774671915,
494869544446107,
75881813291999,
582948691582867,
699080545674263,
026475381780497,
79081463482033,
071155023205776,
63589064122554,
919453166983462,
823699245489316,
41190621774113,
55469303461609,
376153713031748,
964634034459095,
259253799962217,
36845536628347,
889205080921723,
60678513788527,
18384620945546,
439180955075443,
144816617325343,
01588835314883,
12858884432918,
783941551270242,
765874826353908,
508822896380888,
974242428298766,
02934589740598,
65355540733024,
248970638725552,
459221698080256,
026148648672294,
321292043876742,
249285064971772,
776225017519984,
316584881416592,
07140995795683,
057401796842,
545023831101325,
169223505392353,
995355442071453,
787294825599606,
565542080945416,
955701830785966,
669333179960283,
077341508948425,
25776004441367,
389376048426584,
498141677565833,
50339592307222,
322885814343625,
62425773328204,
486809003428295,
159092000580415,
187822780079756,
06443780521571,
243855225614,
211676647446602,
64981467054832,
451652050533625,
538572605411005,
63432278017656,
87021644986186,
98875766066163,
744141033714392,
263594394595493,
9952593748122,
72177009767043,
785367324078905,
20922431097778,
416244563161243,
019871150723027,
86154218534095,
89266829398685,
182067071446887,
71818447906582,
561026436164134,
719465967051388,
521099845823294,
08739035409038,
836398070761803,
464487651350098,
043825682973102,
168952795954556,
610376877674334,
21081192643395,
37962349727399,
216140336463752,
304950345835227,
300740979728843,
069912468399895,
335504206322938,
35285322799954,
337717583632582,
85438767398017,
998879976653816,
156464355062267,
024810935032065,
05128363698332,
059012706316405,
030227227200356,
011018639453859,
539183329989136,
029382922416822,
034821267826826,
823273645678821,
974042015647232,
616191787297623,
67161992288451,
982740907031733,
424027076786718,
49763649613349,
843733221805785,
01555959988555,
29147672389363,
119781031078492,
94494954897806,
59548764773807,
50613885884479,
87416391901549,
061481748856295,
426837574369213,
4221335388918,
724498782755717,
176287308852572,
254971207004957,
542275614774518,
819597338950693,
351365717843965,
197127835817366,
905726779380572,
201714336339773,
032760018611015,
743078602158395,
722401730058728,
856435350439718,
146825731868304,
676695867526192,
03587715369037,
976262320511925,
54106508928413,
728612841448445,
07257105530255,
17007585840977,
377001262439375,
915103850812663,
563788761118147,
98772300351905,
36591789763831,
15916099538556,
149014149159473,
853769272101644,
30039018367316,
590906117707743,
872744386957283,
260588031786344,
15325868767631,
177663848798552,
37776385541281,
88656451820647,
44588586588927,
91804444879507,
280930174644535,
436237432744992,
596771244663984,
331943744855831,
076949040975173,
19702808879159,
874248924790766,
040578759976977,
028946073854833,
730256031728103,
9247978834805,
622365039143027,
53164821811979,
644575172375813,
974726062857066,
758424884541812,
07156014554567,
74029437896872,
64803462601556,
81269211919464,
1124763535701,
249607152463824,
961141303342046,
06851638749137,
503981254522024,
573173350377246,
24798899507361,
66803481538952,
319703715509107,
626334003827438,
645177782949162,
41310592910331,
60614421681267,
82161928437791,
999052097607432,
20714944754795,
201855860793238,
992003210221952,
95383954770761,
10664851259841,
730353755175706,
51442763991529,
098770214339428,
642557839857215,
042232498081496,
63932262716546,
463270283570125,
784174063532504,
28603593554586,
22890494019447,
88551490668133,
80239660961159,
598913643246323,
559739721222098,
5749274108317,
05114409030274,
57306914274723,
636721642682392,
19900001871247,
098181381883336,
176086748287304,
600317813084786,
06068627900864,
903724309905172,
124043825442776,
444336423374928,
090946707668984,
412536198298824,
445827274731645,
34490278878515,
1010635993775,
675108686374042,
07065880861535,
520058705218734,
7171557000151,
186803448184538,
556603006884586,
410127803245416,
180517738410455,
50860826814266,
18248708433372,
276188179843782,
34601966112574,
414071948871634,
521371785460815,
02272640119429,
87137249511945,
928728497952264,
774419656864673,
52466790451539,
369768471872817,
964665881428864,
916480161281985,
500155472410174,
713568763589237,
501708811545157,
492032867894185,
032280444870228,
428513653393924,
87261976529444,
943428352414486,
02443682819398,
17207335380072,
995454801610848,
606674819174092,
462489184043438,
593829608698524,
210732373415333,
50770015702183,
71235520550278,
16358846947371,
91711851460424,
7239170924691,
966860663738693,
79049995861454,
726475868794545,
03798430714655,
55159108807141,
32255524206199,
43319898667044,
795722889429193,
8186288042401,
66618995996261,
445794545629457,
805886786672424,
149409715167177,
00479951449475,
07972543268928,
556867079564995,
97190547073768,
810551078668603,
230420292109862,
87176696584689,
191863510116313,
419803806203575,
19067910845512,
65773834049542,
82554401558806,
43820323539053,
68234021536819,
403542938373555,
885275672445083,
37302014988104,
635931733499202,
994926600976804,
344990734344737,
8887548805691,
168919862375155,
479396285562192,
684913149287034,
78549013124543,
448146686452205,
22382279148738,
017369017183373,
485690935573803,
166717042063617,
70754108193438,
43043103246419,
807771298246195,
358708417367,
446354210566682,
014516296512266,
68830588318673,
308437076615345,
70262436997153,
76134242648656,
442692326014544,
024777450980764,
024653197656596,
175777269682367,
714987367252512,
043301099142159,
169095186670814,
626663314540625,
22307443724571,
852642638194656,
240275483389004,
140730282921433,
027133749745522,
026537375179839,
036049864332849,
025543809097522,
02694823437733,
168532083265,
22456156045198,
732692900092601,
084789371213962,
453915591406663,
704927875988528,
240338415814218,
10740031041127,
76456673709961,
026731729417886,
023701381614742,
047264754858524,
364306821635552,
360340536995867,
967538339289161,
042613531681155,
337237275068976,
340947450013962,
125589991780558,
058619641173774,
122792753875554,
139357790967118,
645271917253847,
024831726199558,
751483485649796,
024669064639454,
63391116553137,
975327846011592,
055152932976723,
226153558418622,
475668813508548,
867344170403964,
068087228172736,
527782272894612,
264458370678259,
20895233542204,
146644345351925,
037700645797372,
849525480519212,
73018712966702,
119323458953378,
74937654227123,
329664661715285,
785038643341075,
9717716531213,
468755164573803,
804540567546765,
36431955360888,
040849537691013,
87879244667936,
360378587617209,
549104027954392,
97571114725552,
589519600605975,
578411400042546,
206114378319208,
067169016406146,
61110640017563,
704177534540385,
305407205678407,
159058319703005,
047434964212826,
708389615368873,
07212983291744,
24904217778611,
64625754360486,
28667550794593,
513440500955593,
32490532969568,
87187820517669,
5939020045517,
107649957374665,
09091700722756,
49161250640463,
00761245260098,
84155111279547,
573225461177355,
169914692562166,
838019643830101,
346053440079956,
36098488570803,
778834129129095,
23702861321717,
503233456388166,
392791368130823,
436980092983152,
162809089039591,
743754462335803,
120225325239543,
39857503345378,
007953950210318,
21008123708441,
83631510981921,
76350168276804,
860737295989722,
979626014629552,
47581083096278,
483695697496934,
413081732468157,
502420728941807,
19787128893807,
028815191979426,
390941336937644,
16469581653897,
378253230486486,
94058872346474,
853342900231702,
002464578670804,
60452130127463,
531659681722495,
23153804229674,
716786420978764,
444152110600324,
77584598214875,
26291971635598,
48780651855774,
993691790591498]

%matplotlib notebook

fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111,projection='3d')

X_ = dataframe[['RM','LSTAT']].values[:,0]
Y_ = dataframe[['RM','LSTAT']].values[:,1]

Z = predicate_results

rm_and_lstp_price = ax.plot_trisurf(X_, Y_, Z, color='green')

ax.set_xlabel('RM')
ax.set_ylabel('% of lower state')
ax.set_zlabel('Predicated-Price')

<IPython.core.display.Javascript object>

Text(0.5, 0, 'Predicated-Price')

如何发布框架呢？

截至目前，我们已经完成了核心代码，接下来如何发布自己的深度学习框架代码呢？

人工智能的几个方向：计算机视觉（Computer Vision）、自然语言处理（Natrual Language Process）、推荐系统(Recommand System)、数据挖掘（Data Mining）都基于神经网络。

Python发布教程
需要的IDE：PyCharm

liscence表示发布代码的版权问题

将代码中和神经网络、神经元相关的部分变为nn中，拓扑排序放入utils中

需要源代码，可以发邮件到minchuian.gao@gmail.com，介绍一下你自己

文档信息

本文作者：weownthenight
本文链接：https://weownthenight.github.io/2021/03/21/%E4%BB%8E%E9%9B%B6%E6%9E%84%E5%BB%BA%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E6%A1%86%E6%9E%B6-%E4%B8%89/
版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）

weownthenight的博客