这节课上要讨论的问题如下:
- What’s the machine learning?
- What’s the k-n-n algorithm?
- What’s the regression?
- What’s the loss function and why it is the key for our machine learning task?
- What’s the Gradient Descent?
Step1: Load Data & Data Analysis
from sklearn.datasets import load_boston
dataset = load_boston()
??dataset #对dataset本身不清楚可以使用??或者help
help(dataset)
Help on Bunch in module sklearn.utils object:
class Bunch(builtins.dict)
| Bunch(**kwargs)
|
| Container object exposing keys as attributes
|
| Bunch objects are sometimes used as an output for functions and methods.
| They extend dictionaries by enabling values to be accessed by key,
| `bunch["value_key"]`, or by an attribute, `bunch.value_key`.
|
| Examples
| --------
| >>> b = Bunch(a=1, b=2)
| >>> b['b']
| 2
| >>> b.b
| 2
| >>> b.a = 3
| >>> b['a']
| 3
| >>> b.c = 6
| >>> b['c']
| 6
|
| Method resolution order:
| Bunch
| builtins.dict
| builtins.object
|
| Methods defined here:
|
| __dir__(self)
| Default dir() implementation.
|
| __getattr__(self, key)
|
| __init__(self, **kwargs)
| Initialize self. See help(type(self)) for accurate signature.
|
| __setattr__(self, key, value)
| Implement setattr(self, name, value).
|
| __setstate__(self, state)
|
| ----------------------------------------------------------------------
| Data descriptors defined here:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
|
| ----------------------------------------------------------------------
| Methods inherited from builtins.dict:
|
| __contains__(self, key, /)
| True if the dictionary has the specified key, else False.
|
| __delitem__(self, key, /)
| Delete self[key].
|
| __eq__(self, value, /)
| Return self==value.
|
| __ge__(self, value, /)
| Return self>=value.
|
| __getattribute__(self, name, /)
| Return getattr(self, name).
|
| __getitem__(...)
| x.__getitem__(y) <==> x[y]
|
| __gt__(self, value, /)
| Return self>value.
|
| __iter__(self, /)
| Implement iter(self).
|
| __le__(self, value, /)
| Return self<=value.
|
| __len__(self, /)
| Return len(self).
|
| __lt__(self, value, /)
| Return self<value.
|
| __ne__(self, value, /)
| Return self!=value.
|
| __repr__(self, /)
| Return repr(self).
|
| __reversed__(self, /)
| Return a reverse iterator over the dict keys.
|
| __setitem__(self, key, value, /)
| Set self[key] to value.
|
| __sizeof__(...)
| D.__sizeof__() -> size of D in memory, in bytes
|
| clear(...)
| D.clear() -> None. Remove all items from D.
|
| copy(...)
| D.copy() -> a shallow copy of D
|
| get(self, key, default=None, /)
| Return the value for key if key is in the dictionary, else default.
|
| items(...)
| D.items() -> a set-like object providing a view on D's items
|
| keys(...)
| D.keys() -> a set-like object providing a view on D's keys
|
| pop(...)
| D.pop(k[,d]) -> v, remove specified key and return the corresponding value.
| If key is not found, d is returned if given, otherwise KeyError is raised
|
| popitem(self, /)
| Remove and return a (key, value) pair as a 2-tuple.
|
| Pairs are returned in LIFO (last-in, first-out) order.
| Raises KeyError if the dict is empty.
|
| setdefault(self, key, default=None, /)
| Insert key with a value of default if key is not in the dictionary.
|
| Return the value for key if key is in the dictionary, else default.
|
| update(...)
| D.update([E, ]**F) -> None. Update D from dict/iterable E and F.
| If E is present and has a .keys() method, then does: for k in E: D[k] = E[k]
| If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v
| In either case, this is followed by: for k in F: D[k] = F[k]
|
| values(...)
| D.values() -> an object providing a view on D's values
|
| ----------------------------------------------------------------------
| Class methods inherited from builtins.dict:
|
| fromkeys(iterable, value=None, /) from builtins.type
| Create a new dictionary with keys from iterable and values set to value.
|
| ----------------------------------------------------------------------
| Static methods inherited from builtins.dict:
|
| __new__(*args, **kwargs) from builtins.type
| Create and return a new object. See help(type) for accurate signature.
|
| ----------------------------------------------------------------------
| Data and other attributes inherited from builtins.dict:
|
| __hash__ = None
dir(dataset)
['DESCR', 'data', 'feature_names', 'filename', 'target']
dataset['feature_names']
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
print(dataset['DESCR']) #通过这个命令可以看到解释,可以看到RM表示房间数量,是第5个特征
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
dataset['data'][:,5] #房间数量是第5个特征,所以用这个命令可以看到
array([6.575, 6.421, 7.185, 6.998, 7.147, 6.43 , 6.012, 6.172, 5.631,
6.004, 6.377, 6.009, 5.889, 5.949, 6.096, 5.834, 5.935, 5.99 ,
5.456, 5.727, 5.57 , 5.965, 6.142, 5.813, 5.924, 5.599, 5.813,
6.047, 6.495, 6.674, 5.713, 6.072, 5.95 , 5.701, 6.096, 5.933,
5.841, 5.85 , 5.966, 6.595, 7.024, 6.77 , 6.169, 6.211, 6.069,
5.682, 5.786, 6.03 , 5.399, 5.602, 5.963, 6.115, 6.511, 5.998,
5.888, 7.249, 6.383, 6.816, 6.145, 5.927, 5.741, 5.966, 6.456,
6.762, 7.104, 6.29 , 5.787, 5.878, 5.594, 5.885, 6.417, 5.961,
6.065, 6.245, 6.273, 6.286, 6.279, 6.14 , 6.232, 5.874, 6.727,
6.619, 6.302, 6.167, 6.389, 6.63 , 6.015, 6.121, 7.007, 7.079,
6.417, 6.405, 6.442, 6.211, 6.249, 6.625, 6.163, 8.069, 7.82 ,
7.416, 6.727, 6.781, 6.405, 6.137, 6.167, 5.851, 5.836, 6.127,
6.474, 6.229, 6.195, 6.715, 5.913, 6.092, 6.254, 5.928, 6.176,
6.021, 5.872, 5.731, 5.87 , 6.004, 5.961, 5.856, 5.879, 5.986,
5.613, 5.693, 6.431, 5.637, 6.458, 6.326, 6.372, 5.822, 5.757,
6.335, 5.942, 6.454, 5.857, 6.151, 6.174, 5.019, 5.403, 5.468,
4.903, 6.13 , 5.628, 4.926, 5.186, 5.597, 6.122, 5.404, 5.012,
5.709, 6.129, 6.152, 5.272, 6.943, 6.066, 6.51 , 6.25 , 7.489,
7.802, 8.375, 5.854, 6.101, 7.929, 5.877, 6.319, 6.402, 5.875,
5.88 , 5.572, 6.416, 5.859, 6.546, 6.02 , 6.315, 6.86 , 6.98 ,
7.765, 6.144, 7.155, 6.563, 5.604, 6.153, 7.831, 6.782, 6.556,
7.185, 6.951, 6.739, 7.178, 6.8 , 6.604, 7.875, 7.287, 7.107,
7.274, 6.975, 7.135, 6.162, 7.61 , 7.853, 8.034, 5.891, 6.326,
5.783, 6.064, 5.344, 5.96 , 5.404, 5.807, 6.375, 5.412, 6.182,
5.888, 6.642, 5.951, 6.373, 6.951, 6.164, 6.879, 6.618, 8.266,
8.725, 8.04 , 7.163, 7.686, 6.552, 5.981, 7.412, 8.337, 8.247,
6.726, 6.086, 6.631, 7.358, 6.481, 6.606, 6.897, 6.095, 6.358,
6.393, 5.593, 5.605, 6.108, 6.226, 6.433, 6.718, 6.487, 6.438,
6.957, 8.259, 6.108, 5.876, 7.454, 8.704, 7.333, 6.842, 7.203,
7.52 , 8.398, 7.327, 7.206, 5.56 , 7.014, 8.297, 7.47 , 5.92 ,
5.856, 6.24 , 6.538, 7.691, 6.758, 6.854, 7.267, 6.826, 6.482,
6.812, 7.82 , 6.968, 7.645, 7.923, 7.088, 6.453, 6.23 , 6.209,
6.315, 6.565, 6.861, 7.148, 6.63 , 6.127, 6.009, 6.678, 6.549,
5.79 , 6.345, 7.041, 6.871, 6.59 , 6.495, 6.982, 7.236, 6.616,
7.42 , 6.849, 6.635, 5.972, 4.973, 6.122, 6.023, 6.266, 6.567,
5.705, 5.914, 5.782, 6.382, 6.113, 6.426, 6.376, 6.041, 5.708,
6.415, 6.431, 6.312, 6.083, 5.868, 6.333, 6.144, 5.706, 6.031,
6.316, 6.31 , 6.037, 5.869, 5.895, 6.059, 5.985, 5.968, 7.241,
6.54 , 6.696, 6.874, 6.014, 5.898, 6.516, 6.635, 6.939, 6.49 ,
6.579, 5.884, 6.728, 5.663, 5.936, 6.212, 6.395, 6.127, 6.112,
6.398, 6.251, 5.362, 5.803, 8.78 , 3.561, 4.963, 3.863, 4.97 ,
6.683, 7.016, 6.216, 5.875, 4.906, 4.138, 7.313, 6.649, 6.794,
6.38 , 6.223, 6.968, 6.545, 5.536, 5.52 , 4.368, 5.277, 4.652,
5. , 4.88 , 5.39 , 5.713, 6.051, 5.036, 6.193, 5.887, 6.471,
6.405, 5.747, 5.453, 5.852, 5.987, 6.343, 6.404, 5.349, 5.531,
5.683, 4.138, 5.608, 5.617, 6.852, 5.757, 6.657, 4.628, 5.155,
4.519, 6.434, 6.782, 5.304, 5.957, 6.824, 6.411, 6.006, 5.648,
6.103, 5.565, 5.896, 5.837, 6.202, 6.193, 6.38 , 6.348, 6.833,
6.425, 6.436, 6.208, 6.629, 6.461, 6.152, 5.935, 5.627, 5.818,
6.406, 6.219, 6.485, 5.854, 6.459, 6.341, 6.251, 6.185, 6.417,
6.749, 6.655, 6.297, 7.393, 6.728, 6.525, 5.976, 5.936, 6.301,
6.081, 6.701, 6.376, 6.317, 6.513, 6.209, 5.759, 5.952, 6.003,
5.926, 5.713, 6.167, 6.229, 6.437, 6.98 , 5.427, 6.162, 6.484,
5.304, 6.185, 6.229, 6.242, 6.75 , 7.061, 5.762, 5.871, 6.312,
6.114, 5.905, 5.454, 5.414, 5.093, 5.983, 5.983, 5.707, 5.926,
5.67 , 5.39 , 5.794, 6.019, 5.569, 6.027, 6.593, 6.12 , 6.976,
6.794, 6.03 ])
Step2: Define the problem
Assuming you were a real state salesperson in Boston. Given some description data about a real state => Its price.
import pandas as pd #为了处理数据方便,使用pandas
Pandas = Panel Data set
可以理解为excel,只是比excel更方便做Python编程
dataframe = pd.DataFrame(dataset['data'])
dataframe.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
len(dataframe) #dataframe一共有多少组数据
506
dataframe
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0.0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1.0 | 273.0 | 21.0 | 391.99 | 9.67 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 |
| 503 | 0.06076 | 0.0 | 11.93 | 0.0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1.0 | 273.0 | 21.0 | 396.90 | 5.64 |
| 504 | 0.10959 | 0.0 | 11.93 | 0.0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1.0 | 273.0 | 21.0 | 393.45 | 6.48 |
| 505 | 0.04741 | 0.0 | 11.93 | 0.0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1.0 | 273.0 | 21.0 | 396.90 | 7.88 |
506 rows × 13 columns
dataframe.columns = dataset['feature_names'] #这组数据特征没有名字,通过这个命令把名字输入
dataframe
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0.0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1.0 | 273.0 | 21.0 | 391.99 | 9.67 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 |
| 503 | 0.06076 | 0.0 | 11.93 | 0.0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1.0 | 273.0 | 21.0 | 396.90 | 5.64 |
| 504 | 0.10959 | 0.0 | 11.93 | 0.0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1.0 | 273.0 | 21.0 | 393.45 | 6.48 |
| 505 | 0.04741 | 0.0 | 11.93 | 0.0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1.0 | 273.0 | 21.0 | 396.90 | 7.88 |
506 rows × 13 columns
dataframe['price'] = dataset['target']
dataframe
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0.0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1.0 | 273.0 | 21.0 | 391.99 | 9.67 | 22.4 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 | 20.6 |
| 503 | 0.06076 | 0.0 | 11.93 | 0.0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1.0 | 273.0 | 21.0 | 396.90 | 5.64 | 23.9 |
| 504 | 0.10959 | 0.0 | 11.93 | 0.0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1.0 | 273.0 | 21.0 | 393.45 | 6.48 | 22.0 |
| 505 | 0.04741 | 0.0 | 11.93 | 0.0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1.0 | 273.0 | 21.0 | 396.90 | 7.88 | 11.9 |
506 rows × 14 columns
Question: What’s the most significant(salient) feature of the house price?
%matplotlib inline
dataframe.corr() #pandas中比较简单的东西,correlation
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CRIM | 1.000000 | -0.200469 | 0.406583 | -0.055892 | 0.420972 | -0.219247 | 0.352734 | -0.379670 | 0.625505 | 0.582764 | 0.289946 | -0.385064 | 0.455621 | -0.388305 |
| ZN | -0.200469 | 1.000000 | -0.533828 | -0.042697 | -0.516604 | 0.311991 | -0.569537 | 0.664408 | -0.311948 | -0.314563 | -0.391679 | 0.175520 | -0.412995 | 0.360445 |
| INDUS | 0.406583 | -0.533828 | 1.000000 | 0.062938 | 0.763651 | -0.391676 | 0.644779 | -0.708027 | 0.595129 | 0.720760 | 0.383248 | -0.356977 | 0.603800 | -0.483725 |
| CHAS | -0.055892 | -0.042697 | 0.062938 | 1.000000 | 0.091203 | 0.091251 | 0.086518 | -0.099176 | -0.007368 | -0.035587 | -0.121515 | 0.048788 | -0.053929 | 0.175260 |
| NOX | 0.420972 | -0.516604 | 0.763651 | 0.091203 | 1.000000 | -0.302188 | 0.731470 | -0.769230 | 0.611441 | 0.668023 | 0.188933 | -0.380051 | 0.590879 | -0.427321 |
| RM | -0.219247 | 0.311991 | -0.391676 | 0.091251 | -0.302188 | 1.000000 | -0.240265 | 0.205246 | -0.209847 | -0.292048 | -0.355501 | 0.128069 | -0.613808 | 0.695360 |
| AGE | 0.352734 | -0.569537 | 0.644779 | 0.086518 | 0.731470 | -0.240265 | 1.000000 | -0.747881 | 0.456022 | 0.506456 | 0.261515 | -0.273534 | 0.602339 | -0.376955 |
| DIS | -0.379670 | 0.664408 | -0.708027 | -0.099176 | -0.769230 | 0.205246 | -0.747881 | 1.000000 | -0.494588 | -0.534432 | -0.232471 | 0.291512 | -0.496996 | 0.249929 |
| RAD | 0.625505 | -0.311948 | 0.595129 | -0.007368 | 0.611441 | -0.209847 | 0.456022 | -0.494588 | 1.000000 | 0.910228 | 0.464741 | -0.444413 | 0.488676 | -0.381626 |
| TAX | 0.582764 | -0.314563 | 0.720760 | -0.035587 | 0.668023 | -0.292048 | 0.506456 | -0.534432 | 0.910228 | 1.000000 | 0.460853 | -0.441808 | 0.543993 | -0.468536 |
| PTRATIO | 0.289946 | -0.391679 | 0.383248 | -0.121515 | 0.188933 | -0.355501 | 0.261515 | -0.232471 | 0.464741 | 0.460853 | 1.000000 | -0.177383 | 0.374044 | -0.507787 |
| B | -0.385064 | 0.175520 | -0.356977 | 0.048788 | -0.380051 | 0.128069 | -0.273534 | 0.291512 | -0.444413 | -0.441808 | -0.177383 | 1.000000 | -0.366087 | 0.333461 |
| LSTAT | 0.455621 | -0.412995 | 0.603800 | -0.053929 | 0.590879 | -0.613808 | 0.602339 | -0.496996 | 0.488676 | 0.543993 | 0.374044 | -0.366087 | 1.000000 | -0.737663 |
| price | -0.388305 | 0.360445 | -0.483725 | 0.175260 | -0.427321 | 0.695360 | -0.376955 | 0.249929 | -0.381626 | -0.468536 | -0.507787 | 0.333461 | -0.737663 | 1.000000 |
Step3: 解决问题
Correlation: 相关性
- 可取-1到1,线性相关
- -1:y = -kx+b
- 1:y = kx+b
import seaborn as sns #可视化工具
sns.heatmap(dataframe.corr(), annot=True, fmt='.2f') #越接近黑色表示负相关,越接近红色表示正相关
<AxesSubplot:>

基于以上分析,我们发现:房屋里卧室的个数与房屋价格最成正相关
简单化:如何依据房屋里卧室的数量来估计房子的面积呢?
在1970s的时候,大家有一个这样的想法
X_rm = dataframe['RM'].values
Y = dataframe['price'].values
rm_to_price = {r: y for r,y in zip(X_rm,Y)} #做一个字典映射
rm_to_price
{6.575: 24.0,
6.421: 21.6,
7.185: 34.9,
6.998: 33.4,
7.147: 36.2,
6.43: 28.7,
6.012: 22.9,
6.172: 27.1,
5.631: 16.5,
6.004: 20.3,
6.377: 15.0,
6.009: 21.7,
5.889: 21.7,
5.949: 20.4,
6.096: 13.5,
5.834: 19.9,
5.935: 8.4,
5.99: 17.5,
5.456: 20.2,
5.727: 18.2,
5.57: 13.6,
5.965: 19.6,
6.142: 15.2,
5.813: 16.6,
5.924: 15.6,
5.599: 13.9,
6.047: 14.8,
6.495: 26.4,
6.674: 21.0,
5.713: 20.1,
6.072: 14.5,
5.95: 13.2,
5.701: 13.1,
5.933: 18.9,
5.841: 20.0,
5.85: 21.0,
5.966: 16.0,
6.595: 30.8,
7.024: 34.9,
6.77: 26.6,
6.169: 25.3,
6.211: 25.0,
6.069: 21.2,
5.682: 19.3,
5.786: 20.0,
6.03: 11.9,
5.399: 14.4,
5.602: 19.4,
5.963: 19.7,
6.115: 20.5,
6.511: 25.0,
5.998: 23.4,
5.888: 23.3,
7.249: 35.4,
6.383: 24.7,
6.816: 31.6,
6.145: 23.3,
5.927: 19.6,
5.741: 18.7,
6.456: 22.2,
6.762: 25.0,
7.104: 33.0,
6.29: 23.5,
5.787: 19.4,
5.878: 22.0,
5.594: 17.4,
5.885: 20.9,
6.417: 13.0,
5.961: 20.5,
6.065: 22.8,
6.245: 23.4,
6.273: 24.1,
6.286: 21.4,
6.279: 20.0,
6.14: 20.8,
6.232: 21.2,
5.874: 20.3,
6.727: 27.5,
6.619: 23.9,
6.302: 24.8,
6.167: 19.9,
6.389: 23.9,
6.63: 27.9,
6.015: 22.5,
6.121: 22.2,
7.007: 23.6,
7.079: 28.7,
6.405: 12.5,
6.442: 22.9,
6.249: 20.6,
6.625: 28.4,
6.163: 21.4,
8.069: 38.7,
7.82: 45.4,
7.416: 33.2,
6.781: 26.5,
6.137: 19.3,
5.851: 19.5,
5.836: 19.5,
6.127: 22.7,
6.474: 19.8,
6.229: 21.4,
6.195: 21.7,
6.715: 22.8,
5.913: 18.8,
6.092: 18.7,
6.254: 18.5,
5.928: 18.3,
6.176: 21.2,
6.021: 19.2,
5.872: 20.4,
5.731: 19.3,
5.87: 22.0,
5.856: 21.1,
5.879: 18.8,
5.986: 21.4,
5.613: 15.7,
5.693: 16.2,
6.431: 24.6,
5.637: 14.3,
6.458: 19.2,
6.326: 24.4,
6.372: 23.0,
5.822: 18.4,
5.757: 15.0,
6.335: 18.1,
5.942: 17.4,
6.454: 17.1,
5.857: 13.3,
6.151: 17.8,
6.174: 14.0,
5.019: 14.4,
5.403: 13.4,
5.468: 15.6,
4.903: 11.8,
6.13: 13.8,
5.628: 15.6,
4.926: 14.6,
5.186: 17.8,
5.597: 15.4,
6.122: 22.1,
5.404: 19.3,
5.012: 15.3,
5.709: 19.4,
6.129: 17.0,
6.152: 8.7,
5.272: 13.1,
6.943: 41.3,
6.066: 24.3,
6.51: 23.3,
6.25: 27.0,
7.489: 50.0,
7.802: 50.0,
8.375: 50.0,
5.854: 10.8,
6.101: 25.0,
7.929: 50.0,
5.877: 23.8,
6.319: 23.8,
6.402: 22.3,
5.875: 50.0,
5.88: 19.1,
5.572: 23.1,
6.416: 23.6,
5.859: 22.6,
6.546: 29.4,
6.02: 23.2,
6.315: 22.3,
6.86: 29.9,
6.98: 29.8,
7.765: 39.8,
6.144: 19.8,
7.155: 37.9,
6.563: 32.5,
5.604: 26.4,
6.153: 29.6,
7.831: 50.0,
6.782: 7.5,
6.556: 29.8,
6.951: 26.7,
6.739: 30.5,
7.178: 36.4,
6.8: 31.1,
6.604: 29.1,
7.875: 50.0,
7.287: 33.3,
7.107: 30.3,
7.274: 34.6,
6.975: 34.9,
7.135: 32.9,
6.162: 13.3,
7.61: 42.3,
7.853: 48.5,
8.034: 50.0,
5.891: 22.6,
5.783: 22.5,
6.064: 24.4,
5.344: 20.0,
5.96: 21.7,
5.807: 22.4,
6.375: 28.1,
5.412: 23.7,
6.182: 25.0,
6.642: 28.7,
5.951: 21.5,
6.373: 23.0,
6.164: 21.7,
6.879: 27.5,
6.618: 30.1,
8.266: 44.8,
8.725: 50.0,
8.04: 37.6,
7.163: 31.6,
7.686: 46.7,
6.552: 31.5,
5.981: 24.3,
7.412: 31.7,
8.337: 41.7,
8.247: 48.3,
6.726: 29.0,
6.086: 24.0,
6.631: 25.1,
7.358: 31.5,
6.481: 23.7,
6.606: 23.3,
6.897: 22.0,
6.095: 20.1,
6.358: 22.2,
6.393: 23.7,
5.593: 17.6,
5.605: 18.5,
6.108: 21.9,
6.226: 20.5,
6.433: 24.5,
6.718: 26.2,
6.487: 24.4,
6.438: 24.8,
6.957: 29.6,
8.259: 42.8,
5.876: 20.9,
7.454: 44.0,
8.704: 50.0,
7.333: 36.0,
6.842: 30.1,
7.203: 33.8,
7.52: 43.1,
8.398: 48.8,
7.327: 31.0,
7.206: 36.5,
5.56: 22.8,
7.014: 30.7,
8.297: 50.0,
7.47: 43.5,
5.92: 20.7,
6.24: 25.2,
6.538: 24.4,
7.691: 35.2,
6.758: 32.4,
6.854: 32.0,
7.267: 33.2,
6.826: 33.1,
6.482: 29.1,
6.812: 35.1,
6.968: 10.4,
7.645: 46.0,
7.923: 50.0,
7.088: 32.2,
6.453: 22.0,
6.23: 20.1,
6.209: 21.4,
6.565: 24.8,
6.861: 28.5,
7.148: 37.3,
6.678: 28.6,
6.549: 27.1,
5.79: 20.3,
6.345: 22.5,
7.041: 29.0,
6.871: 24.8,
6.59: 22.0,
6.982: 33.1,
7.236: 36.1,
6.616: 28.4,
7.42: 33.4,
6.849: 28.2,
6.635: 24.5,
5.972: 20.3,
4.973: 16.1,
6.023: 19.4,
6.266: 21.6,
6.567: 23.8,
5.705: 16.2,
5.914: 17.8,
5.782: 19.8,
6.382: 23.1,
6.113: 21.0,
6.426: 23.8,
6.376: 17.7,
6.041: 20.4,
5.708: 18.5,
6.415: 25.0,
6.312: 21.2,
6.083: 22.2,
5.868: 19.3,
6.333: 22.6,
5.706: 17.1,
6.031: 19.4,
6.316: 22.2,
6.31: 20.7,
6.037: 21.1,
5.869: 19.5,
5.895: 18.5,
6.059: 20.6,
5.985: 19.0,
5.968: 18.7,
7.241: 32.7,
6.54: 16.5,
6.696: 23.9,
6.874: 31.2,
6.014: 17.5,
5.898: 17.2,
6.516: 23.1,
6.939: 26.6,
6.49: 22.9,
6.579: 24.1,
5.884: 18.6,
6.728: 14.9,
5.663: 18.2,
5.936: 13.5,
6.212: 17.8,
6.395: 21.7,
6.112: 22.6,
6.398: 25.0,
6.251: 12.6,
5.362: 20.8,
5.803: 16.8,
8.78: 21.9,
3.561: 27.5,
4.963: 21.9,
3.863: 23.1,
4.97: 50.0,
6.683: 50.0,
7.016: 50.0,
6.216: 50.0,
4.906: 13.8,
4.138: 11.9,
7.313: 15.0,
6.649: 13.9,
6.794: 22.0,
6.38: 9.5,
6.223: 10.2,
6.545: 10.9,
5.536: 11.3,
5.52: 12.3,
4.368: 8.8,
5.277: 7.2,
4.652: 10.5,
5.0: 7.4,
4.88: 10.2,
5.39: 19.7,
6.051: 23.2,
5.036: 9.7,
6.193: 11.0,
5.887: 12.7,
6.471: 13.1,
5.747: 8.5,
5.453: 5.0,
5.852: 6.3,
5.987: 5.6,
6.343: 7.2,
6.404: 12.1,
5.349: 8.3,
5.531: 8.5,
5.683: 5.0,
5.608: 27.9,
5.617: 17.2,
6.852: 27.5,
6.657: 17.2,
4.628: 17.9,
5.155: 16.3,
4.519: 7.0,
6.434: 7.2,
5.304: 12.0,
5.957: 8.8,
6.824: 8.4,
6.411: 16.7,
6.006: 14.2,
5.648: 20.8,
6.103: 13.4,
5.565: 11.7,
5.896: 8.3,
5.837: 10.2,
6.202: 10.9,
6.348: 14.5,
6.833: 14.1,
6.425: 16.1,
6.436: 14.3,
6.208: 11.7,
6.629: 13.4,
6.461: 9.6,
5.627: 12.8,
5.818: 10.5,
6.406: 17.1,
6.219: 18.4,
6.485: 15.4,
6.459: 11.8,
6.341: 14.9,
6.185: 14.6,
6.749: 13.4,
6.655: 15.2,
6.297: 16.1,
7.393: 17.8,
6.525: 14.1,
5.976: 12.7,
6.301: 14.9,
6.081: 20.0,
6.701: 16.4,
6.317: 19.5,
6.513: 20.2,
5.759: 19.9,
5.952: 19.0,
6.003: 19.1,
5.926: 24.5,
6.437: 23.2,
5.427: 13.8,
6.484: 16.7,
6.242: 23.0,
6.75: 23.7,
7.061: 25.0,
5.762: 21.8,
5.871: 20.6,
6.114: 19.1,
5.905: 20.6,
5.454: 15.2,
5.414: 7.0,
5.093: 8.1,
5.983: 20.1,
5.707: 21.8,
5.67: 23.1,
5.794: 18.3,
6.019: 21.2,
5.569: 17.5,
6.027: 16.8,
6.593: 22.4,
6.12: 20.6,
6.976: 23.9}
rm_to_price[6.421] #查询卧室数6.421时卖多少钱
21.6
rm_to_pirce[7] #数据中没有7,无法查询价格
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-48-6a5607440deb> in <module>
----> 1 rm_to_pirce[7]
NameError: name 'rm_to_pirce' is not defined
import numpy as np
#解释dictionary
person_and_age = {
'A周杰伦': 40,
'B刘德华': 60,
'C蔡徐坤': 25
}
list(person_and_age.items())
[('A周杰伦', 40), ('B刘德华', 60), ('C蔡徐坤', 25)]
sorted(person_and_age) #直接进行排序发现是按ABC排序的
['A周杰伦', 'B刘德华', 'C蔡徐坤']
def get_first_item(element):
return element[1]
sorted(person_and_age.items(), key=get_first_item) #如果想以年龄排序,加上items
[('C蔡徐坤', 25), ('A周杰伦', 40), ('B刘德华', 60)]
sorted(person_and_age.items(), key=lambda element:element[1]) #因为这个例子比较简单,也可以改为匿名函数
[('C蔡徐坤', 25), ('A周杰伦', 40), ('B刘德华', 60)]
[age for name, age in sorted(person_and_age.items(), key=lambda e:e[1])[:2]] #获得最小的两个年龄
[25, 40]
np.mean([age for name, age in sorted(person_and_age.items(), key=lambda e:e[1])[:2]]) #获得最小的两个年龄并求平均值
32.5
#在数据中找到离query_x最接近的数据对应的结果
def find_price_by_similar(history_price,query_x, topn=3):
"""
作为一个优秀的工程师/算法工作者
代码的可读性一定是大于简洁性
"""
most_similar_items = sorted(history_price.items(),key = lambda x_y:(x_y[0] - query_x)**2)[:topn]
most_similar_prices = [price for rm, price in most_similar_items]
average_prices = np.mean(most_similar_prices)
return average_prices
#按照query_x与x的距离的平方进行排序,取topn最接近的结果再取平均值
find_price_by_similar(rm_to_price,7)
29.233333333333334
MIT 计算机系一句名言:代码是给人看的,偶尔运行一下
KNN算法
K-Neighbor-Nearest = > KNN
这是一个非常非常经典的机器学习算法
什么是机器学习????
KNN算法的缺点:当数据量很大的时候,对已有数据进行遍历需要很长时间。我们把这样的算法叫Lazy Learning.
KNN这种方法比较低效,在数据比较大的时候(还有其他的一些问题)
More Efficient Learning Way
如果我们能够找到X_rm和 y之间的函数关系,我们每次要计算的时候,输入给这个函数,就能直接获得预测值
拟合函数关系!
import matplotlib.pyplot as plt
plt.scatter(X_rm,Y)
<matplotlib.collections.PathCollection at 0x7ffbe2a7b3d0>
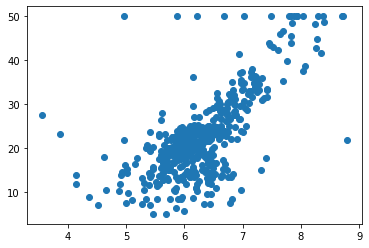
Step4: 评判标准——什么叫做好?
real_y = [3,6,7]
y_hats = [3,4,7]
y_hats_2 = [3,6,6]
Loss函数(今天课程的loss函数叫做 Mean Squared Error:MSE)
\[loss(y,\hat{y}) = \frac{1}{N} {\sum_{i \in N}(y_i - \hat{y_i})^2}\]def loss(y, yhat):
return np.mean((np.array(y)-np.array(yhat)) ** 2)
loss(real_y,y_hats)
1.3333333333333333
loss(real_y,y_hats_2)
0.3333333333333333
我们有了判断标准,那怎么样获得最优的k和b呢?
我们直接用微积分的方法做计算 (当函数极其复杂时,用微积分无法求导得极值)
我们用随机模拟的方法来做
import random
VAR_MAX,VAR_MIN = 100, -100
k, b = random.randint(VAR_MIN,VAR_MAX),random.randint(VAR_MIN,VAR_MAX)
k,b #每次运行都会有一个随机值
(87, 18)
total_times = 500 #总共尝试500次
min_loss = float('inf') #最好的loss无穷大
best_k,best_b = None, None
for t in range(total_times):
k, b = random.randint(VAR_MIN,VAR_MAX),random.randint(VAR_MIN,VAR_MAX)
loss_ = loss(Y,X_rm*k+b)
if loss_ < min_loss:
min_loss = loss_
best_k, best_b = k,b
print('在{}时刻我找到了更好的k:{}和b:{},这个时候的loss是:{}'.format(t,k,b,loss_))
在0时刻我找到了更好的k:23和b:90,这个时候的loss是:45088.61016415613
在1时刻我找到了更好的k:-40和b:86,这个时候的loss是:36544.74020395257
在11时刻我找到了更好的k:11和b:41,这个时候的loss是:7718.814961832015
在13时刻我找到了更好的k:-4和b:-13,这个时候的loss是:3809.19117144664
在33时刻我找到了更好的k:25和b:-98,这个时候的loss是:1506.4455817687747
在35时刻我找到了更好的k:7和b:-45,这个时候的loss是:599.9265171996047
在38时刻我找到了更好的k:-11和b:74,这个时候的loss是:554.7054053102768
在61时刻我找到了更好的k:18和b:-86,这个时候的loss是:103.68217080632411
在173时刻我找到了更好的k:15和b:-69,这个时候的loss是:68.22859204545455
观察得到:In the begining, the updating is more frequent
When time passed by, the updating will be more and more difficult.
针对更新越来越慢的问题,我们考虑怎样才能在后期更新更快?
\[k^{'} = k + (-1)\cdot\frac{\partial loss}{\partial k}\alpha\]解释一下:在一个二维空间里loss-k的函数中,我们求导数,得到导数大于0,就在k的左侧再取下一个k;得到导数小于0,就在k的右侧取下一个k。这里的$ \alpha $是一个很小的数,相当于我们每次都移动一小步。b的估计也可以同理得到。
那么怎么用计算机实现呢?
梯度下降:在二维情况下,我们求的是导数,在多维情况下,就是梯度(Gradient Descent)。
\[loss = \frac{1}{n}\sum (y_i - (kx_i + b))^2\] \[\frac{\partial loss}{\partial k} = \frac{2}{n}\sum(y_i - (kx_i + b))\cdot(-x_i)\] \[\frac{\partial loss}{\partial b} = \frac{2}{n}\sum(y_i - (kx_i + b))\cdot(-1)\]def partial_k(x,y,k_n,b_n):
return 2 * np.mean((y - (k_n * x + b_n)) * (-x))
def partial_b(x,y,k_n,b_n):
return 2 * np.mean((y - (k_n * x + b_n)) * (-1))
%%time
VAR_MAX,VAR_MIN = 100, -100
k, b = random.randint(VAR_MIN,VAR_MAX),random.randint(VAR_MIN,VAR_MAX)
k_b_history = []
total_times = 2000 #总共尝试1000次
min_loss = float('inf') #最好的loss无穷大
best_k,best_b = None, None
alpha = 1e-2
for t in range(total_times):
k = k + (-1) * partial_k(X_rm,Y,k,b) * alpha
b = b + (-1) * partial_b(X_rm,Y,k,b) * alpha
loss_ = loss(Y,X_rm*k+b)
if loss_ < min_loss:
min_loss = loss_
best_k, best_b = k,b
k_b_history.append((best_k,best_b))
#print('在{}时刻我找到了更好的k:{}和b:{},这个时候的loss是:{}'.format(t,k,b,loss_))
CPU times: user 139 ms, sys: 4.06 ms, total: 143 ms
Wall time: 146 ms
这段代码就是深度学习的核心。深度学习的核心就是通过梯度下降的方法获得一组参数,使得loss函数最小。
这样更改后可以看到结果中的loss一直在减小。
min_loss
55.52953732717737
plt.scatter(X_rm,Y)
plt.scatter(X_rm,best_k * X_rm + best_b)
<matplotlib.collections.PathCollection at 0x7ffbe31fdf40>
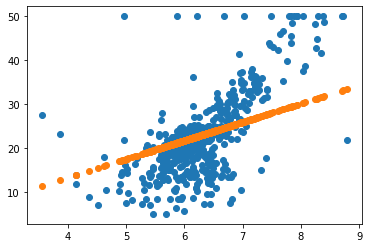
test_0 = 0
test_1 = 10
test_2 = 100
test_3 = 500
test_4 = -1
plt.scatter(X_rm,Y)
plt.scatter(X_rm,k_b_history[test_0][0] * X_rm + k_b_history[test_0][1],color='orange')
plt.scatter(X_rm,k_b_history[test_1][0] * X_rm + k_b_history[test_1][1],color='yellow')
plt.scatter(X_rm,k_b_history[test_2][0] * X_rm + k_b_history[test_2][1],color='red')
plt.scatter(X_rm,k_b_history[test_3][0] * X_rm + k_b_history[test_3][1],color='black')
plt.scatter(X_rm,k_b_history[test_4][0] * X_rm + k_b_history[test_4][1],color='purple')
<matplotlib.collections.PathCollection at 0x7ffbe32f6c10>
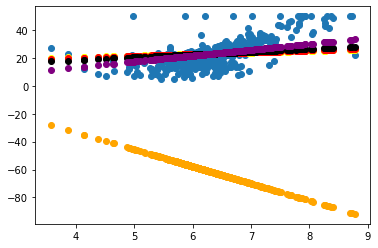
透视了整个获得最优的k和b的过程
best_k * 6 + best_b #用梯度下降的方法得到的预测值
23.990014977139325
%%time
find_price_by_similar(rm_to_price,6) #用knn算法得到的预测值以及运行时间
CPU times: user 692 µs, sys: 7 µs, total: 699 µs
Wall time: 704 µs
20.933333333333334
对比这两个方法的数据可以发现,梯度下降的方法比knn快很多。
Review
什么叫做相关性,通过相关性如何得到最显著的特征
什么叫做机器学习
什么是knn模型
通过随机迭代的方法获得最优值(蒙特卡罗模拟)
什么是loss函数,loss函数能干什么
梯度下降怎么形成的?
展示梯度下降的效果
下节课讲:
如何拟合更加复杂的函数?
什么叫做激活函数(Activation Function)?
什么是神经网络(Neural Network)?
什么是深度学习(Deep Learning)?
什么是反向传播(Back Propogation)?
怎样实现自动反向传播(Auto-Back propogation)?
如何利用拓扑排序(Topologiccal Sorting)让计算机自动进行梯度计算和偏导(Auto-Compute Gradient)?
这些学完就有了构建深度学习框架的元素了。